Lý thuyết Thể tích - Toán 11 Kết nối tri thức
Tổng quan nội dung
Lý thuyết Thể tích - Toán 11 Kết nối tri thức
Chào mừng bạn đến với chuyên mục Lý thuyết Thể tích của môn Toán 11 chương trình Kết nối tri thức tại tusach.vn.
Chuyên mục này cung cấp đầy đủ kiến thức nền tảng về thể tích khối đa diện và khối tròn xoay, giúp bạn hiểu rõ các khái niệm, định lý và công thức quan trọng.
Chúng tôi cam kết mang đến nội dung chính xác, dễ hiểu và có nhiều bài tập thực hành để bạn có thể áp dụng kiến thức vào giải quyết các bài toán thực tế.
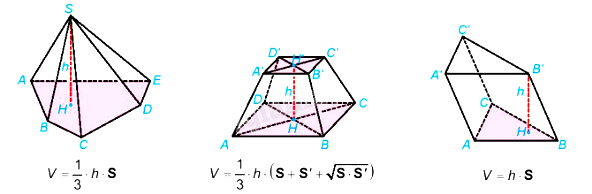
Phần không gian được giới hạn bởi hình chóp, hình chóp cụt đều, hình lăng trụ, hình hộp tương ứng được gọi là khối chóp, khối chóp cụt đều, khối lăng trụ, khối hộp.
Phần không gian được giới hạn bởi hình chóp, hình chóp cụt đều, hình lăng trụ, hình hộp tương ứng được gọi là khối chóp, khối chóp cụt đều, khối lăng trụ, khối hộp. Đỉnh, mặt, cạnh, đường cao của các khối hình đó lần lượt là đỉnh, mặt, cạnh, đường cao của hình chóp, hình chóp cụt đều, hình lăng trụ, hình hộp tương ứng.
- Thể tích của khối chóp có diện tích đáy S và đường cao h là \(V = \frac{1}{3}.h.S\).
- Thể tích của khối chóp cụt đều có diện tích đáy lớn S, diện tích đáy bé S’ và chiều cao h là \(V = \frac{1}{3}.h.\left( {S + S' + \sqrt {S.S'} } \right)\).
- Thể tích của khối lăng trụ có diện tích đáy S và chiều cao h là \(V = h.S\).
Nhận xét:
- Thể tích khối tứ diện bằng một phần ba tích của chiều cao từ một đỉnh và diện tích mặt đối diện với đỉnh đó.
- Thể tích của khối hộp bằng tích của diện tích một mặt và chiều cao của khối hộp tương ứng với mặt đó.
Lý Thuyết Thể Tích - Toán 11 Kết Nối Tri Thức: Tổng Quan và Ứng Dụng
Chào mừng các em học sinh lớp 11 đến với chuyên mục lý thuyết thể tích trong chương trình Toán 11 Kết nối tri thức. Đây là một phần kiến thức quan trọng, không chỉ xuất hiện thường xuyên trong các bài kiểm tra, thi học kỳ mà còn là nền tảng cho các kiến thức nâng cao hơn trong chương trình học.
1. Khái Niệm Cơ Bản về Thể Tích
Thể tích của một vật thể là lượng không gian mà vật thể đó chiếm giữ. Trong hình học không gian, chúng ta thường quan tâm đến thể tích của các khối đa diện và khối tròn xoay. Để tính thể tích, chúng ta cần hiểu rõ các khái niệm như:
- Khối đa diện: Là hình tạo bởi một tập hữu hạn các đa giác phẳng (mặt đa giác) nối với nhau theo các cạnh.
- Khối tròn xoay: Là hình tạo bởi một hình phẳng khi quay quanh một trục.
2. Thể Tích Khối Đa Diện
Để tính thể tích của một khối đa diện, chúng ta thường sử dụng công thức:
V = h.B
Trong đó:
- V là thể tích của khối đa diện.
- B là diện tích đáy của khối đa diện.
- h là chiều cao của khối đa diện (khoảng cách từ đỉnh đến mặt đáy).
Một số khối đa diện thường gặp và công thức tính thể tích:
- Khối chóp: V = (1/3).h.B
- Khối lăng trụ: V = h.B
3. Thể Tích Khối Tròn Xoay
Để tính thể tích của một khối tròn xoay, chúng ta thường sử dụng phương pháp tích phân. Tuy nhiên, đối với một số khối tròn xoay đơn giản, chúng ta có thể sử dụng các công thức sau:
- Khối cầu: V = (4/3).π.R3 (R là bán kính)
- Khối trụ: V = π.R2.h (R là bán kính đáy, h là chiều cao)
- Khối nón: V = (1/3).π.R2.h (R là bán kính đáy, h là chiều cao)
4. Bài Tập Vận Dụng và Mở Rộng
Để nắm vững lý thuyết, các em cần luyện tập giải nhiều bài tập khác nhau. Dưới đây là một số dạng bài tập thường gặp:
- Tính thể tích của khối đa diện khi biết các kích thước.
- Tính thể tích của khối tròn xoay khi biết các thông số.
- Chứng minh các đẳng thức liên quan đến thể tích.
- Ứng dụng kiến thức về thể tích để giải các bài toán thực tế.
5. Mẹo Học Tập và Luyện Thi
- Nắm vững các định nghĩa và công thức: Đây là nền tảng để giải quyết mọi bài toán.
- Vẽ hình minh họa: Giúp các em hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
- Luyện tập thường xuyên: Giải càng nhiều bài tập, các em càng trở nên thành thạo.
- Sử dụng các tài liệu tham khảo: Sách giáo khoa, sách bài tập, các trang web học trực tuyến như tusach.vn là những nguồn tài liệu hữu ích.
6. Bảng Tổng Hợp Công Thức Thể Tích
| Khối | Công Thức |
|---|---|
| Chóp | V = (1/3).h.B |
| Lăng trụ | V = h.B |
| Cầu | V = (4/3).π.R3 |
| Trụ | V = π.R2.h |
| Nón | V = (1/3).π.R2.h |
Hy vọng với những kiến thức và hướng dẫn trên, các em sẽ học tốt môn Toán 11 và đạt kết quả cao trong các kỳ thi. Chúc các em thành công!