Giải mục 1 trang 81, 82 SGK Toán 11 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải Mục 1 Trang 81, 82 SGK Toán 11 Tập 2 - Kết Nối Tri Thức
Chào mừng các em học sinh đến với lời giải chi tiết Mục 1 trang 81, 82 SGK Toán 11 tập 2 - Kết nối tri thức trên tusach.vn. Chúng tôi hiểu rằng việc tự học và làm bài tập đôi khi gặp nhiều khó khăn.
Do đó, tusach.vn luôn cố gắng cung cấp những lời giải chính xác, dễ hiểu, giúp các em học tập hiệu quả và đạt kết quả tốt nhất.
Một vật di chuyển trên một đường thẳng (H.9.2).
HĐ 1
Video hướng dẫn giải
Một vật di chuyển trên một đường thẳng (H.9.2). Quãng đường s của chuyển động là một hàm số của thời gian t, s = s(t) (được gọi là phương trình của chuyển động).
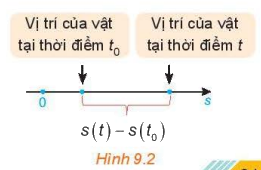
a) Tính vận tốc trung bình của vật trong khoảng thời gian từ t0 đến t.
b Giới hạn \(\mathop {\lim }\limits_{t \to {t_0}} \frac{{s\left( t \right) - s\left( {{t_0}} \right)}}{{t - {t_0}}}\) cho ta biết điều gì?
Phương pháp giải:
Vận tốc trung bình bằng tổng quãng đường đi được chia cho thời gian chuyển động
Lời giải chi tiết:
a) Vận tốc trung bình của vật trong khoảng thời gian từ t0 đến t là \({v_{tb}} = \frac{{s\left( t \right) - s\left( {{t_0}} \right)}}{{t - {t_0}}}\)
b) Khi t càng gần t0, tức là \(\left| {t - {t_0}} \right|\) càng nhỏ thì vận tốc trung bình càng thể hiện được chính xác hơn mức độ nhanh chậm của chuyển động tại thời điểm t0.
HĐ 2
Video hướng dẫn giải
Điện lượng Q truyền trong dây dẫn là một hàm số của thời gian t, có dạng Q = Q(t).
a) Tính cường độ trung bình của dòng điện trong khoảng thời gian từ t0 đến t.
b) Giới hạn \(\mathop {\lim }\limits_{t \to {t_0}} \frac{{Q\left( t \right) - Q\left( {{t_0}} \right)}}{{t - {t_0}}}\) cho ta biết điều gì?
Phương pháp giải:
Cường độ trung bình của dòng điện là thương số giữa điện lượng chuyển qua bề mặt trong khoảng thời gian đó và khoảng thời gian đang xét.
Lời giải chi tiết:
a) Cường độ trung bình của dòng điện trong khoảng thời gian từ t0 đến t là \({I_{tb}} = \frac{{Q\left( t \right) - Q\left( {{t_0}} \right)}}{{t - {t_0}}}\)
b) Khi t càng gần t0, tức là \(\left| {t - {t_0}} \right|\) càng nhỏ thì cường độ trung bình càng thể hiện được chính xác hơn cường độ dòng điện tại thời điểm t0.
Giải Mục 1 Trang 81, 82 SGK Toán 11 Tập 2 - Kết Nối Tri Thức: Tổng Quan và Phương Pháp Giải
Mục 1 trang 81, 82 SGK Toán 11 tập 2 - Kết nối tri thức tập trung vào việc ôn tập chương 3: Hàm số lượng giác và ứng dụng của hàm số lượng giác. Đây là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững các kiến thức về hàm số lượng giác, đồ thị hàm số lượng giác, phương trình lượng giác và các ứng dụng thực tế của chúng.
Nội Dung Chính của Mục 1
Mục 1 bao gồm các bài tập tổng hợp, giúp học sinh rèn luyện kỹ năng giải toán và củng cố kiến thức đã học. Các dạng bài tập thường gặp bao gồm:
- Xác định tập xác định của hàm số lượng giác: Yêu cầu học sinh phải hiểu rõ điều kiện xác định của các hàm số lượng giác (sin, cos, tan, cot) và áp dụng vào giải bài tập.
- Tìm tập giá trị của hàm số lượng giác: Dựa vào đồ thị hàm số lượng giác và các tính chất của hàm số để xác định tập giá trị.
- Giải phương trình lượng giác: Sử dụng các công thức lượng giác cơ bản, các phương pháp biến đổi phương trình và các kỹ năng giải phương trình để tìm nghiệm.
- Ứng dụng hàm số lượng giác vào giải bài toán thực tế: Ví dụ như tính chiều cao của một tòa nhà, khoảng cách giữa hai điểm, hoặc giải các bài toán liên quan đến dao động điều hòa.
Hướng Dẫn Giải Chi Tiết Các Bài Tập
Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu trong Mục 1 trang 81, 82 SGK Toán 11 tập 2 - Kết nối tri thức:
Bài 1: Tìm tập xác định của hàm số y = tan(2x + π/3)
Để tìm tập xác định của hàm số y = tan(2x + π/3), ta cần giải điều kiện: 2x + π/3 ≠ π/2 + kπ (k ∈ Z). Từ đó suy ra x ≠ π/12 + kπ/2 (k ∈ Z). Vậy tập xác định của hàm số là D = R \ {π/12 + kπ/2 | k ∈ Z}.
Bài 2: Giải phương trình sin(x) = 1/2
Phương trình sin(x) = 1/2 có hai họ nghiệm là:
- x = π/6 + k2π (k ∈ Z)
- x = 5π/6 + k2π (k ∈ Z)
Mẹo Giải Toán Lượng Giác Hiệu Quả
Để giải các bài tập toán lượng giác một cách hiệu quả, các em có thể tham khảo một số mẹo sau:
- Nắm vững các công thức lượng giác cơ bản: Các công thức cộng, trừ, nhân, chia, hạ bậc, nâng bậc, và các công thức biến đổi lượng giác khác.
- Sử dụng đồ thị hàm số lượng giác: Đồ thị hàm số lượng giác giúp các em hình dung được tính chất của hàm số và tìm nghiệm một cách dễ dàng hơn.
- Biến đổi phương trình lượng giác về dạng cơ bản: Sử dụng các công thức lượng giác để biến đổi phương trình về dạng sin(x) = a, cos(x) = a, tan(x) = a, hoặc cot(x) = a.
- Kiểm tra lại nghiệm: Sau khi tìm được nghiệm, hãy kiểm tra lại nghiệm bằng cách thay vào phương trình ban đầu để đảm bảo tính chính xác.
Tusach.vn – Đồng Hành Cùng Học Sinh
Tusach.vn luôn đồng hành cùng các em học sinh trên con đường chinh phục kiến thức. Ngoài lời giải chi tiết Mục 1 trang 81, 82 SGK Toán 11 tập 2 - Kết nối tri thức, chúng tôi còn cung cấp lời giải cho tất cả các bài tập trong SGK và SBT Toán 11, cũng như các tài liệu học tập hữu ích khác. Hãy truy cập tusach.vn để được hỗ trợ tốt nhất!
| Chương | Bài | Nội Dung |
|---|---|---|
| 3 | Mục 1 | Ôn tập chương 3 |