Bài 4.5 Trang 77 Toán 11 Tập 1 - Kết Nối Tri Thức

Bài 4.5 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức

Bài 4.5 trang 77 SGK Toán 11 Tập 1 - Kết Nối Tri Thức

Bài 4.5 trang 77 SGK Toán 11 Tập 1 thuộc chương trình học Toán 11 Kết Nối Tri Thức. Bài học này tập trung vào việc giải quyết các bài toán liên quan đến vectơ, đặc biệt là các bài toán ứng dụng trong hình học.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.

Cho hình chóp tứ giác S.ABCD và lấy một điểm E thuộc cạnh SA của hình chóp (E khác S, A).Trong mặt phẳng (ABCD) vẽ một đường thằng d cắt các cạnh CB, CD lần lượt tại M, N và cắt các tia AB, AD lần lượt tại P, Q.

Đề bài

Cho hình chóp tứ giác S.ABCD và lấy một điểm E thuộc cạnh SA của hình chóp (E khác S, A).Trong mặt phẳng (ABCD) vẽ một đường thằng d cắt các cạnh CB, CD lần lượt tại M, N và cắt các tia AB, AD lần lượt tại P, Q.

a) Xác định giao điểm của mp (E,d) với các cạnh SB, SD của hình chóp.

b) Xác định giao tuyến của mp (E,d) với các mặt của hình chóp.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Bài 4.5 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức 1

Để xác định giao điểm của một đường thẳng và một mặt phẳng, ta có thể tìm giao điểm của đường thẳng đó với một đường thẳng nằm trong mặt phẳng đã cho.

Để chứng minh giao tuyến của hai mặt phẳng, ta tìm hai điểm cùng thuộc cả hai mặt phẳng đó.

Lời giải chi tiết

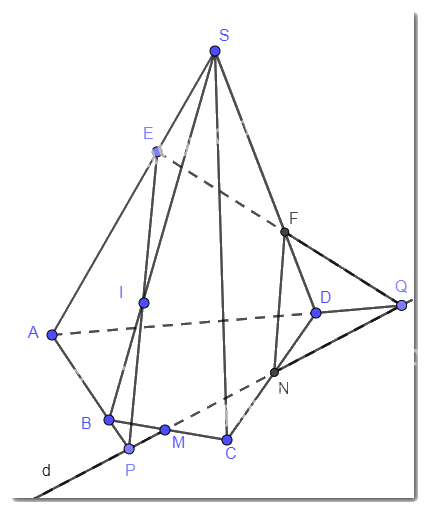
Bài 4.5 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức 2

- Giao điểm của mp(E,d) với cạnh SB

P thuộc AB suy ra P cũng thuộc mp(SAB)

Trên mp(SAB), gọi giao điểm của EP và SB là I

P thuộc đường thẳng d suy ra P cũng nằm trên mp(E,d)

E, P đều nằm trên mp(D,d) suy ra EP nằm trên mp(E,d) suy ra I cũng nằm trên mp(E,d)

Vậy I là giao điểm của mp(E,d) và SB

- Giao điểm của mp(E,d) với cạnh SD.

Q thuộc AD suy ra Q nằm trên mp(SAD)

Gọi giao điểm của EQ và SD là F

Q thuộc đường thẳng d suy ra Q cũng nằm trên mp(E,d)

E, Q đều nằm trên mp(E,d) suy ra EQ nằm trên mp(E,d) , suy ra F cũng nằm trên mp(E,d)

Vậy F là giao điểm của mp(E,d) và SD.

b) Ta có EI cùng thuộc mp(SAB) và mp(E,d) suy ra EI là tuyến điểm của hai mặt phẳng.

EF cùng thuộc mp(SAD) và mp(E,d) suy ra EF là giao tuyến của hai mặt phẳng

\(IM \subset mp\left( {SBC} \right),IM \subset mp\left( {E,d} \right)\) suy ra IM là giao tuyến của hai mp(SBC) và mp(E,d).

\(FN \subset mp\left( {SCD} \right),FN \subset mp\left( {E,d} \right)\) suy ra FN là giao tuyến của mp(SCD) và mp(E,d).

Bài 4.5 Trang 77 SGK Toán 11 Tập 1 - Kết Nối Tri Thức: Giải Chi Tiết và Hướng Dẫn

Bài 4.5 trang 77 SGK Toán 11 Tập 1 - Kết Nối Tri Thức là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về vectơ và ứng dụng của chúng trong hình học. Dưới đây là giải chi tiết bài tập này, cùng với những hướng dẫn và lưu ý quan trọng để bạn có thể tự tin giải quyết các bài toán tương tự.

Nội dung bài tập 4.5 trang 77 SGK Toán 11 Tập 1 - Kết Nối Tri Thức

Bài tập yêu cầu chúng ta sử dụng kiến thức về vectơ để chứng minh một số tính chất hình học, thường liên quan đến các điểm, đường thẳng và các hình đa giác. Để giải bài tập này, bạn cần nắm vững các khái niệm cơ bản về vectơ như:

Vectơ: Định nghĩa, các phép toán trên vectơ (cộng, trừ, nhân với một số).
Tích vô hướng của hai vectơ: Cách tính, ứng dụng để tính góc giữa hai vectơ, kiểm tra tính vuông góc.
Hệ tọa độ: Biểu diễn vectơ trong hệ tọa độ, các phép toán trên vectơ trong hệ tọa độ.

Giải chi tiết bài tập 4.5 trang 77 SGK Toán 11 Tập 1 - Kết Nối Tri Thức

(Ở đây sẽ là lời giải chi tiết cho bài tập 4.5, bao gồm các bước giải, giải thích rõ ràng và sử dụng hình vẽ minh họa nếu cần thiết. Ví dụ, nếu bài tập yêu cầu chứng minh một tứ giác là hình bình hành, lời giải sẽ trình bày các bước chứng minh dựa trên tính chất của vectơ, ví dụ như chứng minh hai cặp cạnh đối song song hoặc bằng nhau.)

Ví dụ minh họa và bài tập tương tự

Để giúp bạn hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ xem xét một ví dụ minh họa:

Ví dụ: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2.

Lời giải:

Vì M là trung điểm của BC, ta có overrightarrow{BM} =overrightarrow{MC}.
overrightarrow{AM} =overrightarrow{AB} +overrightarrow{BM}
overrightarrow{AM} =overrightarrow{AC} +overrightarrow{CM} =overrightarrow{AC} -overrightarrow{MC}
Cộng hai phương trình trên, ta được: 2overrightarrow{AM} =overrightarrow{AB} +overrightarrow{AC}
Suy ra: overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2 (đpcm)

Ngoài ra, bạn có thể tham khảo thêm các bài tập tương tự sau:

Bài tập 4.6 trang 77 SGK Toán 11 Tập 1 - Kết Nối Tri Thức
Bài tập 4.7 trang 78 SGK Toán 11 Tập 1 - Kết Nối Tri Thức

Lưu ý khi giải bài tập về vectơ

Khi giải các bài tập về vectơ, bạn cần lưu ý những điều sau:

Vẽ hình minh họa để dễ dàng hình dung bài toán.
Sử dụng các tính chất của vectơ một cách linh hoạt.
Kiểm tra lại kết quả sau khi giải xong.

Tổng kết

Bài 4.5 trang 77 SGK Toán 11 Tập 1 - Kết Nối Tri Thức là một bài tập quan trọng giúp bạn củng cố kiến thức về vectơ và ứng dụng của chúng trong hình học. Hy vọng với lời giải chi tiết và những hướng dẫn trên, bạn sẽ tự tin giải quyết bài tập này và các bài tập tương tự một cách hiệu quả. Hãy luyện tập thường xuyên để nắm vững kiến thức và kỹ năng giải toán nhé!