Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Lý thuyết Công thức lượng giác - SGK Toán 11 Kết nối tri thức
SGK Toán 11 - Kết nối tri thức
Toán 11 tập 1 - Kết nối tri thức với cuộc sống
Chương 1 Hàm số lượng giác và phương trình lượng giác
Bài 2. Công thức lượng giác

Lý thuyết Công thức lượng giác - SGK Toán 11 Kết nối tri thức

Lý Thuyết Công Thức Lượng Giác - Toán 11 Kết Nối Tri Thức

Chào mừng bạn đến với chuyên mục lý thuyết công thức lượng giác của chương trình Toán 11 Kết Nối Tri Thức trên tusach.vn.

Ở đây, chúng tôi cung cấp một cách tiếp cận toàn diện và dễ hiểu về các khái niệm, định nghĩa và công thức lượng giác quan trọng.

Mục tiêu của chúng tôi là giúp bạn nắm vững kiến thức nền tảng, tự tin giải quyết các bài tập và đạt kết quả tốt nhất trong học tập.

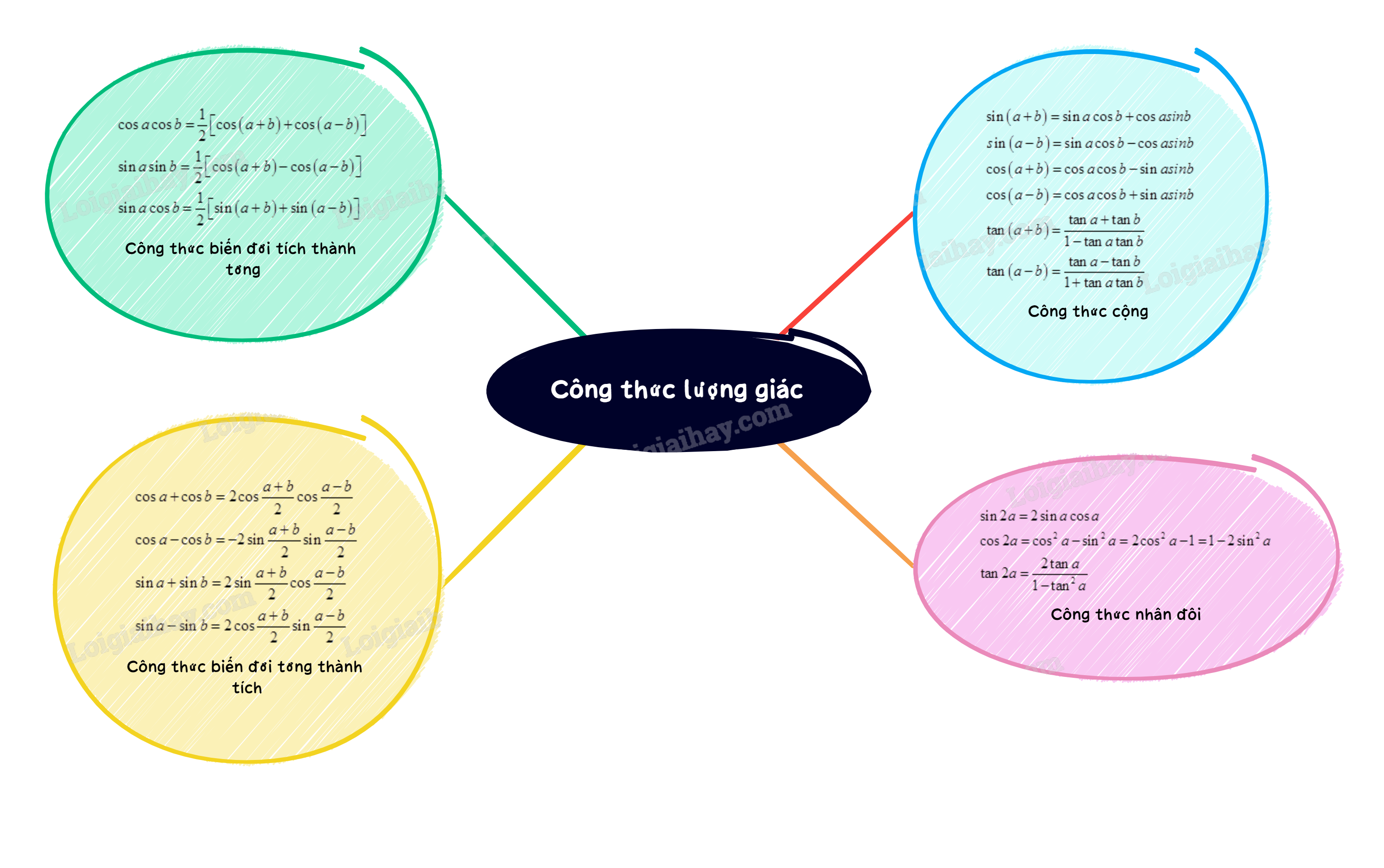
1. Công thức cộng

1. Công thức cộng

\(\begin{array}{l}\sin \left( {a + b} \right) = \sin a\cos b + \cos asinb\\sin\left( {a - b} \right) = \sin a\cos b - \cos asinb\\\cos \left( {a + b} \right) = \cos a\cos b - \sin asinb\\\cos \left( {a - b} \right) = \cos a\cos b + \sin asinb\\\tan \left( {a + b} \right) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\\\tan \left( {a - b} \right) = \frac{{\tan a - \tan b}}{{1 + \tan a\tan b}}\end{array}\)

2. Công thức nhân đôi

\(\begin{array}{l}\sin 2a = 2\sin a\cos a\\\cos 2a = {\cos ^2}a - {\sin ^2}a = 2{\cos ^2}a - 1 = 1 - 2{\sin ^2}a\\\tan 2a = \frac{{2\tan a}}{{1 - {{\tan }^2}a}}\end{array}\)

Suy ra, công thức hạ bậc:

\({\sin ^2}a = \frac{{1 - \cos 2a}}{2},{\cos ^2}a = \frac{{1 + \cos 2a}}{2}\)

3. Công thức biến đổi tích thành tổng

\(\begin{array}{l}\cos a\cos b = \frac{1}{2}\left[ {\cos \left( {a + b} \right) + \cos \left( {a - b} \right)} \right]\\\sin a\sin b = \frac{1}{2}\left[ {\cos \left( {a - b} \right) - \cos \left( {a + b} \right)} \right]\\\sin a\cos b = \frac{1}{2}\left[ {\sin \left( {a + b} \right) + \sin \left( {a - b} \right)} \right]\end{array}\)

4. Công thức biến đổi tổng thành tích

\(\begin{array}{l}\cos a + \cos b = 2\cos \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\\\cos a - \cos b = - 2\sin \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\\\sin a + \sin b = 2\sin \frac{{a + b}}{2}\cos \frac{{a - b}}{2}\\\sin a - \sin b = 2\cos \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\end{array}\)

Lý thuyết Công thức lượng giác - SGK Toán 11 Kết nối tri thức 1

Lý Thuyết Công Thức Lượng Giác - Toán 11 Kết Nối Tri Thức: Tổng Quan

Chương trình Toán 11 Kết Nối Tri Thức đi sâu vào lĩnh vực lượng giác, một nhánh quan trọng của toán học có ứng dụng rộng rãi trong nhiều lĩnh vực như vật lý, kỹ thuật, và khoa học máy tính. Việc nắm vững lý thuyết và công thức lượng giác là nền tảng để giải quyết các bài toán phức tạp và hiểu rõ hơn về thế giới xung quanh.

1. Góc Lượng Giác và Đơn Vị Đo Góc

Góc lượng giác được định nghĩa là một hình được tạo thành bởi hai tia chung gốc gọi là các cạnh của góc. Đơn vị đo góc phổ biến nhất là độ (°), radian (rad), và grad (g). Việc chuyển đổi giữa các đơn vị này là rất quan trọng trong các bài toán lượng giác.

  • 1° = π/180 rad
  • 1 rad = 180/π °

2. Hàm Số Lượng Giác

Hàm số lượng giác là các hàm số liên hệ giữa góc và tỷ số các cạnh của tam giác vuông. Các hàm số lượng giác cơ bản bao gồm:

  • Sin (sin α): Tỷ số giữa cạnh đối và cạnh huyền.
  • Cosin (cos α): Tỷ số giữa cạnh kề và cạnh huyền.
  • Tangent (tan α): Tỷ số giữa cạnh đối và cạnh kề.
  • Cotangent (cot α): Tỷ số giữa cạnh kề và cạnh đối.

3. Các Công Thức Lượng Giác Cơ Bản

Có rất nhiều công thức lượng giác cần được ghi nhớ và áp dụng trong quá trình giải toán. Dưới đây là một số công thức quan trọng:

3.1. Công Thức Lượng Giác Cơ Bản

Công ThứcMô Tả
sin2 α + cos2 α = 1Định lý Pytago lượng giác
tan α = sin α / cos αMối quan hệ giữa tan, sin và cos
cot α = cos α / sin αMối quan hệ giữa cot, sin và cos

3.2. Công Thức Cộng và Hiệu Góc

  • sin(α + β) = sin α cos β + cos α sin β
  • sin(α - β) = sin α cos β - cos α sin β
  • cos(α + β) = cos α cos β - sin α sin β
  • cos(α - β) = cos α cos β + sin α sin β

3.3. Công Thức Nhân Đôi

  • sin 2α = 2 sin α cos α
  • cos 2α = cos2 α - sin2 α = 2cos2 α - 1 = 1 - 2sin2 α

4. Ứng Dụng của Lý Thuyết Lượng Giác

Lý thuyết lượng giác có ứng dụng rộng rãi trong nhiều lĩnh vực:

  • Giải tam giác: Tính các cạnh và góc của tam giác khi biết một số thông tin nhất định.
  • Vật lý: Mô tả các hiện tượng dao động, sóng, và chuyển động tròn.
  • Kỹ thuật: Thiết kế các công trình xây dựng, máy móc, và hệ thống điều khiển.
  • Định vị và đo đạc: Xác định vị trí và khoảng cách giữa các đối tượng.

5. Luyện Tập và Bài Tập

Để nắm vững lý thuyết và công thức lượng giác, bạn cần luyện tập thường xuyên với các bài tập khác nhau. tusach.vn cung cấp một bộ sưu tập bài tập đa dạng và phong phú, kèm theo đáp án và lời giải chi tiết. Hãy truy cập trang Bài tập Lượng giác Toán 11 Kết Nối Tri Thức để bắt đầu luyện tập ngay hôm nay!

Kết Luận

Lý thuyết công thức lượng giác là một phần quan trọng của chương trình Toán 11 Kết Nối Tri Thức. Hy vọng rằng, với những kiến thức và hướng dẫn trên, bạn sẽ tự tin hơn trong việc học tập và giải quyết các bài toán liên quan đến lượng giác. Chúc bạn thành công!

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN