Lý thuyết Giới hạn của hàm số - SGK Toán 11 Kết nối tri thức
Tổng quan nội dung
Lý thuyết Giới hạn của hàm số - Nền tảng Toán 11
Lý thuyết Giới hạn của hàm số là một trong những nội dung quan trọng bậc nhất trong chương trình Toán 11 Kết nối tri thức.
Chủ đề này đặt nền móng cho việc học các khái niệm nâng cao hơn như đạo hàm, tích phân trong các lớp học tiếp theo.
1. Giới hạn hữu hạn của hàm số tại một điểm
1. Giới hạn hữu hạn của hàm số tại một điểm
Giả sử (a;b) là một khoảng chứa điểm \({x_0}\)và hàm số \(y = f(x)\)xác định trên khoảng (a;b), có thể trừ điểm \({x_0}\). Ta nói hàm số \(f(x)\)có giới hạn là số L khi \(x\) dần tới \({x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\)bất kì, \({x_n} \in \left( {a;b} \right)\),\({x_n} \ne {x_0}\) và \({x_n} \to {x_0}\), ta có\(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\)hay \(f(x) \to L\), khi \({x_n} \to {x_0}\).
*Quy tắc tính giới hạn của hàm số tại một điểm
a, Nếu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\)và \(\mathop {\lim }\limits_{x \to {x_0}} g(x) = M\)thì
\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x) \pm g(x)} \right] = L \pm M\)
\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f(x).g(x)} \right] = L.M\)
\(\mathop {\lim }\limits_{x \to {x_0}} \left[ {\frac{{f(x)}}{{g(x)}}} \right] = \frac{L}{M}\left( {M \ne 0} \right)\)
b, Nếu \(f(x) \ge 0\)với mọi \(x \in \left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}\) và \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = L\) thì \(L \ge 0\)và \(\mathop {\lim }\limits_{x \to {x_0}} \sqrt {f(x)} = \sqrt L \).
2. Giới hạn một bên
Cho hàm số \(y = f(x)\)xác định trên khoảng \(\left( {{x_0};b} \right)\). Ta nói số L là giới hạn bên phải của \(f(x)\)khi \(x \to {x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\)bất kì thỏa mãn \({x_0} < {x_n} < b\) và \({x_n} \to {x_0}\)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = L\).
Cho hàm số \(y = f(x)\)xác định trên khoảng \(\left( {a;{x_0}} \right)\). Ta nói số L là giới hạn bên trái của khi \(x \to {x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\)bất kì thỏa mãn \(a < {x_n} < {x_0}\) và \({x_n} \to {x_0}\)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = L\).
3. Giới hạn hữu hạn của hàm số tại vô cực
Cho hàm số \(y = f(x)\)xác định trên khoảng \(\left( {a; + \infty } \right)\). Ta nói hàm số \(f(x)\)có giới hạn là số L khi \(x \to + \infty \) nếu với dãy số \(\left( {{x_n}} \right)\)bất kì \({x_n} > a\) và \({x_n} \to + \infty \)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = L\) hay \(f(x) \to L\) khi \(x \to + \infty \).
Cho hàm số \(y = f(x)\)xác định trên khoảng \(\left( { - \infty ;b} \right)\). Ta nói hàm số \(f(x)\)có giới hạn là số L khi \(x \to - \infty \) nếu với dãy số \(\left( {{x_n}} \right)\)bất kì \({x_n} < b\) và \({x_n} \to - \infty \)ta có \(f({x_n}) \to L\), kí hiệu \(\mathop {\lim }\limits_{x \to - \infty } f(x) = L\) hay \(f(x) \to L\) khi \(x \to - \infty \).
* Nhận xét:
Các quy tắc tính giới hạn hữu hạn tại một điểm cũng đúng cho giới hạn hữu hạn tại vô cực.
Với c là hằng số, \(\mathop {\lim }\limits_{x \to + \infty } c = c\), \(\mathop {\lim }\limits_{x \to - \infty } c = c\).
Với k là một số nguyên dương, ta có: \(\mathop {\lim }\limits_{x \to + \infty } (\frac{1}{{{x^k}}}) = 0,\mathop {\lim }\limits_{x \to - \infty } (\frac{1}{{{x^k}}}) = 0\).
4. Giới hạn vô cực của hàm số tại một điểm
a, Giới hạn vô cực
- Giả sử (a;b) là một khoảng chứa \({x_0}\)và hàm số \(y = f(x)\)xác định trên khoảng \(\left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}\). Ta nói hàm số \(f(x)\)có giới hạn là \( + \infty \)khi \(x\) dần tới \({x_0}\) nếu với dãy số \(\left( {{x_n}} \right)\)bất kì, \(\left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}\) và \({x_n} \to {x_0}\), ta có\(f({x_n}) \to + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = + \infty \).
Ta nói hàm số \(f(x)\)có giới hạn \( - \infty \)khi \(x \to {x_0}\), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) = - \infty \), nếu \(\mathop {\lim }\limits_{x \to {x_0}} \left[ { - f(x)} \right] = + \infty \).
- Cho hàm số \(y = f(x)\)xác định trên khoảng \(\left( {{x_0};b} \right)\). Ta nói hàm số \(f(x)\)có giới hạn \( + \infty \) khi \(x \to {x_0}\) về bên phải nếu với dãy số \(\left( {{x_n}} \right)\)bất kì thỏa mãn \({x_0} < {x_n} < b\) và \({x_n} \to {x_0}\)ta có \(f({x_n}) \to + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = + \infty \).
Cho hàm số \(y = f(x)\)xác định trên khoảng \(\left( {a;{x_0}} \right)\). Ta nói hàm số \(f(x)\)có giới hạn \( + \infty \) khi \(x \to {x_0}\) về bên trái nếu với dãy số \(\left( {{x_n}} \right)\)bất kì thỏa mãn \(a < {x_n} < {x_0}\) và \({x_n} \to {x_0}\)ta có \(f({x_n}) \to + \infty \), kí hiệu \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = + \infty \).
Các giới hạn một bên\(\mathop {\lim }\limits_{x \to {x_0}^ + } f(x) = - \infty \), \(\mathop {\lim }\limits_{x \to {x_0}^ - } f(x) = - \infty \) được định nghĩa tương tự.
b, Một số quy tắc tính giới hạn vô cực
*Giới hạn của tích\(\mathop {\lim }\limits_{x \to {x_0}} f(x).g(x)\)

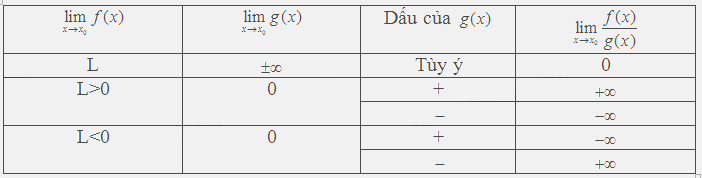
*Giới hạn của thương \(\frac{{f(x)}}{{g(x)}}\)
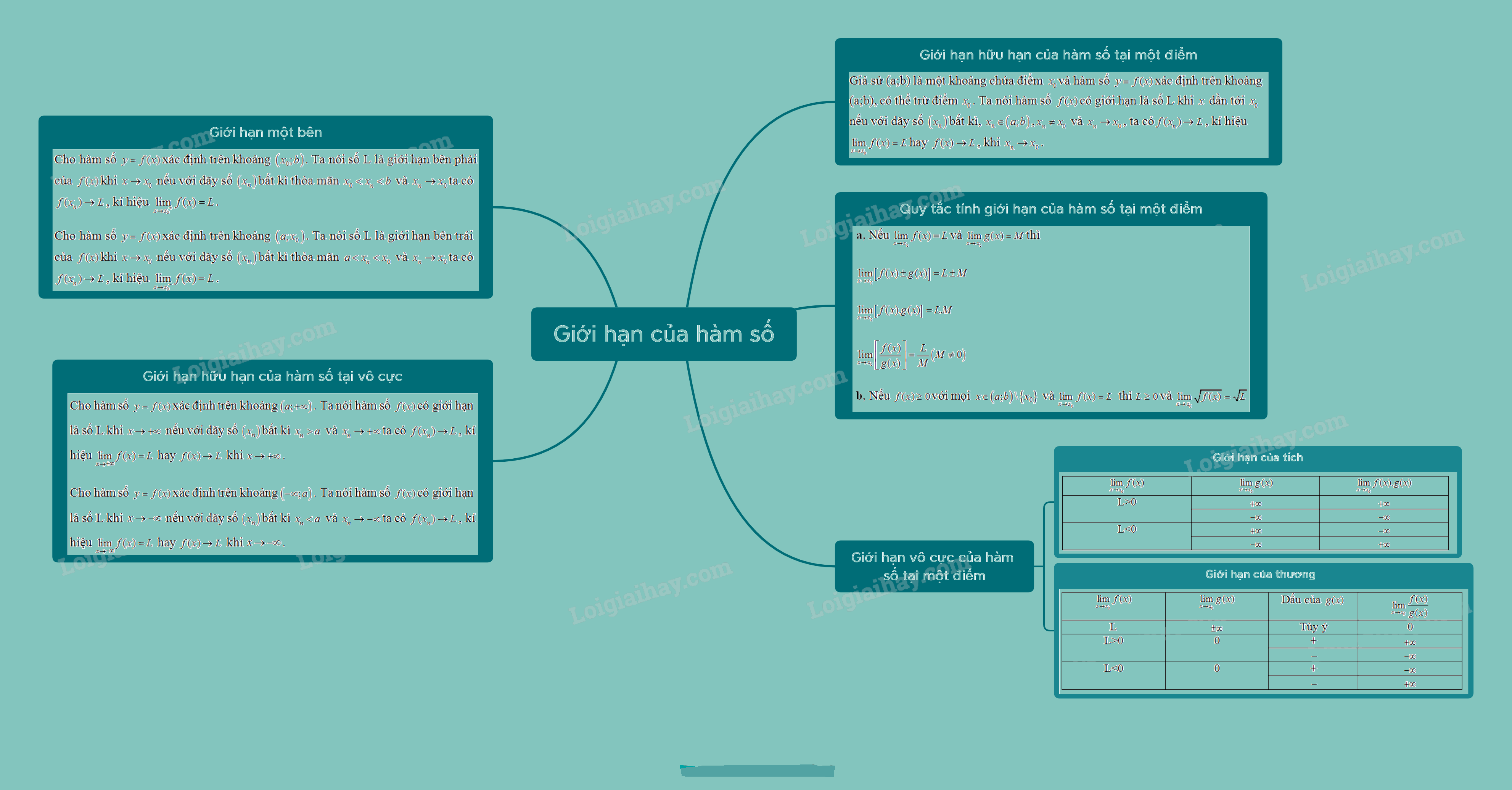
Lý Thuyết Giới Hạn của Hàm Số - Toán 11 Kết Nối Tri Thức: Giải Mã Từng Khái Niệm
Chào mừng các em học sinh đến với bài học về Lý thuyết Giới hạn của hàm số, một chủ đề then chốt trong chương trình Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp một cái nhìn toàn diện về khái niệm giới hạn, các tính chất, và cách áp dụng chúng vào giải quyết các bài toán cụ thể.
1. Khái Niệm Giới Hạn của Hàm Số
Giới hạn của hàm số tại một điểm là giá trị mà hàm số tiến tới khi biến số độc lập tiến tới điểm đó. Nói cách khác, nó mô tả hành vi của hàm số khi chúng ta đến gần một giá trị cụ thể của biến số.
Ký hiệu: limx→a f(x) = L, trong đó:
- x → a: x tiến tới a
- f(x): Hàm số cần tính giới hạn
- L: Giá trị giới hạn
2. Các Loại Giới Hạn
Có hai loại giới hạn chính:
- Giới hạn hữu hạn: Khi x tiến tới a, f(x) tiến tới một giá trị hữu hạn L.
- Giới hạn vô cùng: Khi x tiến tới a, f(x) tiến tới vô cùng dương hoặc vô cùng âm.
3. Tính Chất của Giới Hạn
Việc nắm vững các tính chất của giới hạn sẽ giúp chúng ta đơn giản hóa việc tính toán giới hạn một cách hiệu quả:
- Giới hạn của tổng: lim (f(x) + g(x)) = lim f(x) + lim g(x)
- Giới hạn của tích: lim (f(x) * g(x)) = lim f(x) * lim g(x)
- Giới hạn của thương: lim (f(x) / g(x)) = (lim f(x)) / (lim g(x)) (với lim g(x) ≠ 0)
- Giới hạn của hằng số: lim c = c (với c là hằng số)
4. Các Dạng Bài Tập Thường Gặp
Dưới đây là một số dạng bài tập thường gặp liên quan đến giới hạn hàm số:
- Tính giới hạn của hàm đa thức: Thay trực tiếp giá trị của x vào hàm số.
- Tính giới hạn của hàm phân thức: Phân tích tử và mẫu thành nhân tử, rút gọn biểu thức, sau đó thay giá trị của x.
- Tính giới hạn của hàm lượng giác: Sử dụng các công thức lượng giác và giới hạn đặc biệt.
- Tính giới hạn vô cùng: Phân tích biểu thức và sử dụng các quy tắc tính giới hạn vô cùng.
5. Ví Dụ Minh Họa
Ví dụ 1: Tính limx→2 (x2 + 3x - 1)
Giải: Thay x = 2 vào hàm số, ta được: 22 + 3*2 - 1 = 4 + 6 - 1 = 9. Vậy limx→2 (x2 + 3x - 1) = 9.
Ví dụ 2: Tính limx→1 (x2 - 1) / (x - 1)
Giải: Phân tích tử thành nhân tử: (x2 - 1) = (x - 1)(x + 1). Vậy limx→1 (x2 - 1) / (x - 1) = limx→1 (x + 1) = 1 + 1 = 2.
6. Luyện Tập và Củng Cố Kiến Thức
Để nắm vững kiến thức về giới hạn hàm số, các em nên luyện tập thường xuyên với các bài tập khác nhau. Các em có thể tìm thấy nhiều bài tập và tài liệu tham khảo trên tusach.vn.
Bảng tổng hợp các giới hạn đặc biệt:
| Giới hạn | Giá trị |
|---|---|
| limx→0 sin(x)/x | 1 |
| limx→0 (1 - cos(x))/x | 0 |
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về Lý thuyết Giới hạn của hàm số trong chương trình Toán 11 Kết nối tri thức. Chúc các em học tập tốt!