Giải mục 1 trang 54, 55 SGK Toán 11 tập 2 - Kết nối tri thức

Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 54, 55 sách giáo khoa Toán 11 tập 2 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em học sinh hiểu rõ các khái niệm, định lý và phương pháp giải bài tập liên quan.

Chúng tôi luôn cố gắng cung cấp nội dung chính xác và đầy đủ nhất để hỗ trợ quá trình học tập của các em.

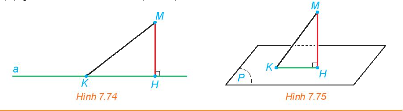
a) Cho điểm M và đường thẳng a. Gọi H là hình chiếu của M trên a. Với mỗi điểm K thuộc a, vì sao MK ≥ MH (H.7.74)

HĐ 1

Video hướng dẫn giải

a) Cho điểm M và đường thẳng a. Gọi H là hình chiếu của M trên a. Với mỗi điểm K thuộc a, vì sao MK ≥ MH (H.7.74)

b) Cho điểm M và mặt phẳng (P). Gọi H là hình chiếu của M trên (P). Với mỗi điểm K thuộc (P), giải thích vì sao MK ≥ MH (H.7.75).

Giải mục 1 trang 54, 55 SGK Toán 11 tập 2 - Kết nối tri thức 1

Phương pháp giải:

Dựa vào mối quan hệ đường xiên và đường vuông góc.

Lời giải chi tiết:

a) Vì H là hình chiếu của M trên đường thẳng a, nên MH là khoảng cách từ M đến a và MH là đoạn thẳng ngắn nhất từ M đến a, suy ra MK ≥ MH.

b) Vì H là hình chiếu của M trên (P) nên MH vuông góc với (P) do đó MH vuông góc với HK.

Dựa vào mối quan hệ đường xiên và đường vuông góc ta có MK ≥ MH.

LT 1

Video hướng dẫn giải

Cho hình lăng trụ đứng ABC.A'B'C' có ABC là tam giác vuông cân tại A, AB = a, AA' = h (H.7.77).

a) Tính khoảng cách từ A đến mặt phẳng (BCC'B').

b) Tam giác ABC' là tam giác gì? Tính khoảng cách từ A đến BC'.

Giải mục 1 trang 54, 55 SGK Toán 11 tập 2 - Kết nối tri thức 1

Phương pháp giải:

- Khoảng cách từ một điểm M đến một đường thẳng a, kí hiệu d (M, a), là khoảng cách giữa M và hình chiếu H của M trên a.

- Khoảng cách từ một điểm M đến một mặt phẳng (P), kí hiệu d (M, (P)), là khoảng cách giữa M và hình chiếu H của M trên (P).

Lời giải chi tiết:

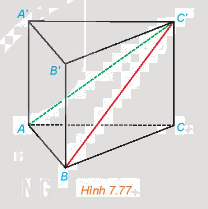
Giải mục 1 trang 54, 55 SGK Toán 11 tập 2 - Kết nối tri thức 2

a) Ta có \(BB' \bot \left( {ABC} \right);BB' \subset \left( {BCC'B'} \right) \Rightarrow \left( {ABC} \right) \bot \left( {BCC'B'} \right)\)

\(\left( {ABC} \right) \cap \left( {BCC'B'} \right) = BC\)

(ABC): Kẻ \(AH \bot BC\)

\( \Rightarrow AH \bot \left( {BCC'B'} \right) \Rightarrow d\left( {A,\left( {BCC'B'} \right)} \right) = AH\)

Xét tam giác ABC vuông cân tại A có

\(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{2}{{{a^2}}}\) (hệ thức lượng trong tam giác vuông)

\( \Rightarrow AH = \frac{{a\sqrt 2 }}{2}\)

b) +) Ta có \(AB \bot AC,AB \bot AA'\left( {AA' \bot \left( {ABC} \right)} \right) \Rightarrow AB \bot \left( {ACC'A'} \right);AC' \subset \left( {ACC'A'} \right) \Rightarrow AC' \bot AB\)

Do đó tam giác ABC' là tam giác vuông.

+) Trên (ABC’) kẻ \(AK \bot BC' \Rightarrow d\left( {A,BC'} \right) = AK\)

Xét tam giác ACC’ vuông tại C có

\(A{C'^2} = A{C^2} + C{C'^2} = {a^2} + {h^2}\) (Định lí Pytago)

Xét tam giác ABC’ vuông tại A có

\(\begin{array}{l}\frac{1}{{A{K^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{{C'}^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{a^2} + {h^2}}} = \frac{{2{a^2} + {h^2}}}{{{a^2}\left( {{a^2} + {h^2}} \right)}} \Rightarrow A{K^2} = \frac{{{a^2}\left( {{a^2} + {h^2}} \right)}}{{2{a^2} + {h^2}}}\\ \Rightarrow AK = a.\sqrt {\frac{{{a^2} + {h^2}}}{{2{a^2} + {h^2}}}} \end{array}\)

Giải mục 1 trang 54, 55 SGK Toán 11 tập 2 - Kết nối tri thức: Tổng quan và Phương pháp giải

Mục 1 trang 54, 55 SGK Toán 11 tập 2 - Kết nối tri thức tập trung vào việc ôn tập chương 3: Hàm số lượng giác và ứng dụng của hàm số lượng giác. Đây là một phần quan trọng trong chương trình Toán 11, đòi hỏi học sinh phải nắm vững các kiến thức về hàm số lượng giác, đồ thị hàm số lượng giác, phương trình lượng giác và ứng dụng của chúng vào giải quyết các bài toán thực tế.

Nội dung chính của Mục 1

Ôn tập lý thuyết: Hệ thống lại các kiến thức cơ bản về hàm số lượng giác (sin, cos, tan, cot), tập xác định, tập giá trị, tính tuần hoàn, tính chẵn lẻ, đồ thị hàm số lượng giác.
Phương pháp giải phương trình lượng giác: Ôn tập các phương pháp giải phương trình lượng giác cơ bản như phương pháp đặt ẩn phụ, phương pháp sử dụng công thức lượng giác, phương pháp biến đổi phương trình về dạng cơ bản.
Ứng dụng của hàm số lượng giác: Giải các bài toán liên quan đến ứng dụng của hàm số lượng giác trong việc khảo sát và giải quyết các vấn đề thực tế.

Giải chi tiết các bài tập trong Mục 1

Dưới đây là lời giải chi tiết cho các bài tập trong Mục 1 trang 54, 55 SGK Toán 11 tập 2 - Kết nối tri thức:

Bài 1: (Trang 54)

(Nội dung bài tập và lời giải chi tiết)

Bài 2: (Trang 54)

(Nội dung bài tập và lời giải chi tiết)

Bài 3: (Trang 55)

(Nội dung bài tập và lời giải chi tiết)

Phương pháp giải bài tập hiệu quả

Để giải các bài tập trong Mục 1 một cách hiệu quả, các em học sinh cần:

Nắm vững lý thuyết: Hiểu rõ các khái niệm, định lý và công thức lượng giác.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập.
Sử dụng các công cụ hỗ trợ: Sử dụng máy tính bỏ túi, phần mềm vẽ đồ thị hàm số lượng giác để kiểm tra kết quả và hiểu rõ hơn về đồ thị hàm số.
Tham khảo các nguồn tài liệu: Tham khảo sách giáo khoa, sách bài tập, các trang web học tập trực tuyến để tìm kiếm thêm thông tin và lời giải.

Lưu ý quan trọng

Khi giải các bài tập về hàm số lượng giác, các em cần chú ý đến:

Đơn vị đo góc: Đảm bảo sử dụng đúng đơn vị đo góc (độ hoặc radian).
Tập xác định của hàm số: Xác định đúng tập xác định của hàm số để tránh các lỗi sai.
Sử dụng công thức lượng giác: Áp dụng đúng các công thức lượng giác để biến đổi và giải phương trình.

Kết luận

Hy vọng rằng với lời giải chi tiết và phương pháp giải hiệu quả mà tusach.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc giải các bài tập trong Mục 1 trang 54, 55 SGK Toán 11 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!

Giải mục 1 trang 54, 55 SGK Toán 11 tập 2 - Kết nối tri thức

Giải mục 1 trang 54, 55 SGK Toán 11 tập 2 - Kết nối tri thức

HĐ 1

LT 1

Giải mục 1 trang 54, 55 SGK Toán 11 tập 2 - Kết nối tri thức: Tổng quan và Phương pháp giải

Nội dung chính của Mục 1

Giải chi tiết các bài tập trong Mục 1

Bài 1: (Trang 54)

Bài 2: (Trang 54)

Bài 3: (Trang 55)

Phương pháp giải bài tập hiệu quả

Lưu ý quan trọng

Kết luận

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN