Giải mục 1 trang 16, 17 SGK Toán 11 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải mục 1 trang 16, 17 SGK Toán 11 tập 2 - Kết nối tri thức
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 11 tập 2 - Kết nối tri thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tốt nhất để giúp bạn học tập hiệu quả.
Bài giải này tập trung vào mục 1, trang 16 và 17, giúp bạn hiểu rõ các khái niệm và phương pháp giải bài tập liên quan.
a) Tính (y = {2^x}) khi x lần lượt nhận các giá trị - 1; 0; 1. Với mỗi giá trị của x có bao nhiêu giá trị của (y = {2^x}) tương ứng?
HĐ 1
Video hướng dẫn giải
a) Tính \(y = {2^x}\) khi x lần lượt nhận các giá trị - 1; 0; 1. Với mỗi giá trị của x có bao nhiêu giá trị của \(y = {2^x}\) tương ứng?
b) Với những giá trị nào của x, biểu thức \(y = {2^x}\) có nghĩa?
Phương pháp giải:
Thay các giá trị x lần lượt để tính y.
Lời giải chi tiết:
a) Với \(x = - 1\) thì \(y = {2^{ - 1}} = \frac{1}{2}\)
Với \(x = 0\) thì \(y = {2^0} = 1\)
Với \(x = 1\) thì \(y = {2^1} = 2\)
b) Biểu thức \(y = {2^x}\) có nghĩa với mọi giá trị của x.
CH
Video hướng dẫn giải
Trong các hàm số sau, những hàm số nào là hàm số mũ? Khi đó hãy chỉ ra cơ cố.
a) \(y = {\left( {\sqrt 2 } \right)^x};\)
b) \(y = {2^{ - x}};\)
c) \(y = {8^{\frac{x}{3}}};\)
d) \(y = {x^{ - 2}}.\)
Phương pháp giải:
Sử dụng định nghĩa hàm số mũ.
Lời giải chi tiết:
a) \(y = {\left( {\sqrt 2 } \right)^x}\) là hàm số mũ có cơ số là \(\sqrt 2 .\)
b) \(y = {2^{ - x}} = {\left( {{2^{ - 1}}} \right)^x}\) là hàm số mũ có cơ số là \({2^{ - 1}} = \frac{1}{2}.\)
c) \(y = {8^{\frac{x}{3}}} = {\left( {{8^{\frac{1}{3}}}} \right)^x} = {\left( {\sqrt[3]{8}} \right)^x}\) là hàm số mũ có cơ số là \({8^{\frac{1}{3}}} = \sqrt[3]{8} = 2.\)
d) \(y = {x^{ - 2}}\) không là hàm số mũ.
HĐ 2
Video hướng dẫn giải
Cho hàm số mũ \(y = {2^x}.\)
a) Hoàn thành bảng giá trị sau:

b) Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; 2x) với \(x \in \mathbb{R}\) và nối lại ta được đồ thị của hàm số
c) Từ đồ thị đã vẽ ở câu b, hãy kết luận về tập giá trị và tính chất biến thiên của hàm số
Phương pháp giải:
Vẽ đồ thị dựa vào các điểm đã lấy sau đó nhìn đồ thị để đưa ra tập giá trị và tính chất biến thiên.
Lời giải chi tiết:
a)

b,
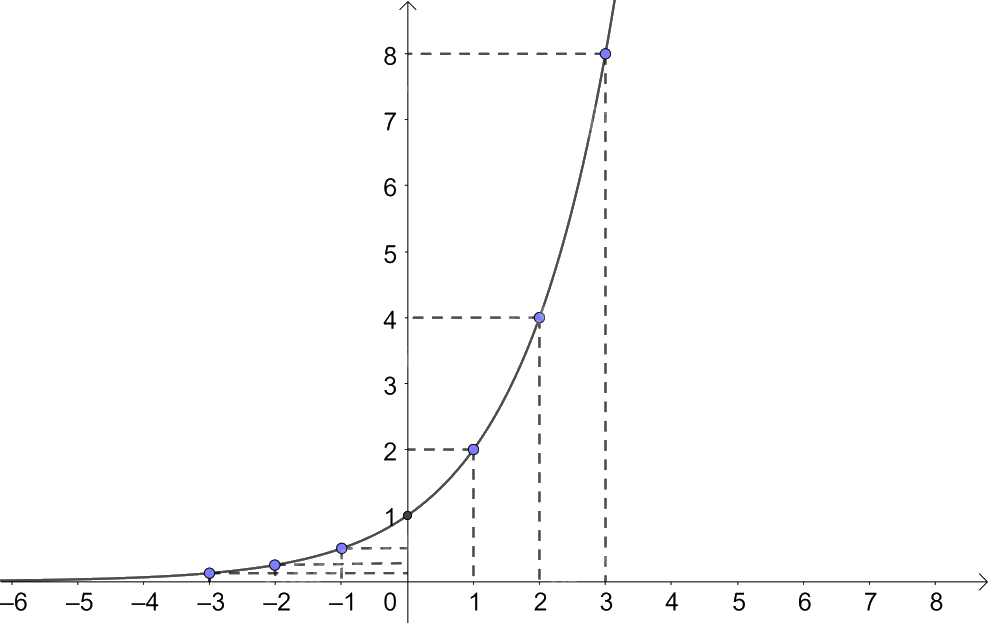
c) Tập giá trị: \(\left( {0; + \infty } \right)\)
Tính chất biến thiên: đồng biến
LT
Video hướng dẫn giải
Vẽ đồ thị của hàm số \(y = {\left( {\frac{3}{2}} \right)^x}.\)
Phương pháp giải:
Lập bảng giá trị để vẽ đồ thị hàm số.
Lời giải chi tiết:
Lập bảng giá trị của hàm số tại một điểm như sau:

Từ đó, ta vẽ được đồ thị của hàm số:

Giải mục 1 trang 16, 17 SGK Toán 11 tập 2 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 1 của chương trình Toán 11 tập 2 - Kết nối tri thức tập trung vào các kiến thức cơ bản về đạo hàm của hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học. Bài viết này sẽ cung cấp lời giải chi tiết cho các bài tập trong SGK trang 16 và 17, đồng thời phân tích phương pháp giải và các lưu ý quan trọng.
Nội dung chính của Mục 1
- Đạo hàm của hàm số tại một điểm: Định nghĩa, ý nghĩa hình học và các tính chất cơ bản.
- Đạo hàm của hàm số: Định nghĩa, điều kiện đạo hàm tồn tại.
- Các quy tắc tính đạo hàm: Đạo hàm của tổng, hiệu, tích, thương và hàm hợp.
- Đạo hàm của một số hàm số cơ bản: Hàm số lũy thừa, hàm số mũ, hàm số logarit, hàm số lượng giác.
Giải chi tiết các bài tập trang 16, 17 SGK Toán 11 tập 2 - Kết nối tri thức
Bài 1: Tính đạo hàm của các hàm số sau tại điểm x = x0
Bài tập này yêu cầu học sinh vận dụng định nghĩa đạo hàm để tính đạo hàm của hàm số tại một điểm cụ thể. Cần lưu ý sử dụng đúng công thức và thực hiện các phép tính cẩn thận.
Ví dụ: Tính đạo hàm của hàm số f(x) = x2 + 1 tại x = 2.
Giải:
- f'(x) = limh→0 [f(x+h) - f(x)] / h
- f'(x) = limh→0 [(x+h)2 + 1 - (x2 + 1)] / h
- f'(x) = limh→0 [x2 + 2xh + h2 + 1 - x2 - 1] / h
- f'(x) = limh→0 [2xh + h2] / h
- f'(x) = limh→0 [2x + h]
- f'(x) = 2x
- f'(2) = 2 * 2 = 4
Bài 2: Tính đạo hàm của các hàm số sau
Bài tập này yêu cầu học sinh sử dụng các quy tắc tính đạo hàm để tìm đạo hàm của hàm số. Cần xác định đúng quy tắc áp dụng cho từng hàm số và thực hiện các phép tính chính xác.
Ví dụ: Tính đạo hàm của hàm số y = 3x4 - 2x2 + 5.
Giải:
y' = 12x3 - 4x
Bài 3: Tìm đạo hàm của hàm số y = (x2 + 1) / (x - 1)
Bài tập này yêu cầu học sinh sử dụng quy tắc đạo hàm của thương. Cần áp dụng đúng công thức và thực hiện các phép tính cẩn thận.
Lưu ý khi giải bài tập về đạo hàm
- Nắm vững định nghĩa đạo hàm và ý nghĩa hình học của đạo hàm.
- Hiểu rõ các quy tắc tính đạo hàm và điều kiện áp dụng.
- Thực hành giải nhiều bài tập để làm quen với các dạng bài khác nhau.
- Kiểm tra lại kết quả sau khi giải bài tập.
Hy vọng với lời giải chi tiết và phương pháp giải được trình bày trong bài viết này, các bạn học sinh sẽ tự tin hơn khi giải các bài tập về đạo hàm trong SGK Toán 11 tập 2 - Kết nối tri thức. Chúc các bạn học tập tốt!
Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ.