Giải mục 4 trang 47, 48 SGK Toán 11 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải mục 4 trang 47, 48 SGK Toán 11 tập 2 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 4 trang 47, 48 sách giáo khoa Toán 11 tập 2 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em học sinh hiểu rõ các khái niệm, định lý và phương pháp giải bài tập liên quan.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và đầy đủ nhất để hỗ trợ các em trong quá trình học tập.
Một tài liệu hướng dẫn rằng đối với ghế bàn ăn, nên thiết kế lưng ghế tạo với mặt ghế một góc có số đo từ 100° đến 105°.
HĐ5
Video hướng dẫn giải
Một tài liệu hướng dẫn rằng đối với ghế bàn ăn, nên thiết kế lưng ghế tạo với mặt ghế một góc có số đo từ 100° đến 105°. Trong Hình 7.51, các tia Ox, Oy được vẽ tương ứng trên mặt ghế, lưng ghế đồng thời vuông góc với giao tuyến a của mặt ghế và lưng ghế.
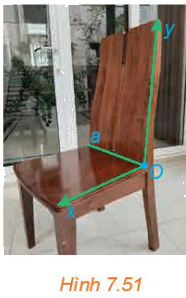
a) Theo tài liệu nói trên, góc nào trong hình nên có số đo từ 100° đến 105°?
b) Nếu thiết kế theo hướng dẫn đó thì góc giữa mặt phẳng chứa mặt ghế và mặt phẳng chứa lưng ghế có thể nhận số đo từ bao nhiêu đến bao nhiêu độ?
Phương pháp giải:
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng vuông góc vào giao tuyến hai mặt phẳng tại cùng một điểm.
Lời giải chi tiết:
a) Theo tài liệu nói trên, góc xOy trong hình nên có số đo từ 100° đến 105°
b) Vì các tia Ox, Oy được vẽ tương ứng trên mặt ghế, lưng ghế đồng thời vuông góc với giao tuyến a của mặt ghế và lưng ghế nên góc giữa lưng ghế và mặt ghế là góc giữa Ox và Oy mà góc xOy có số đo từ 100° đến 105°
Do đó nếu thiết kế theo hướng dẫn đó thì góc giữa mặt phẳng chứa mặt ghế và mặt phẳng chứa lưng ghế có thể nhận số đo 750 đến 800
LT4
Video hướng dẫn giải
Cho hình chóp S.ABC có SA \( \bot \) (ABC), AB = AC = a, \(\widehat {BAC} = {120^0},SA = \frac{a}{{2\sqrt 3 }}.\) Gọi M là trung điểm của BC.

a) Chứng minh rằng \(\widehat {SMA}\) là một góc phẳng của góc nhị diện [S, BC, A].
b) Tính số đo của góc nhị diện [S, BC, A].
Phương pháp giải:
Từ một điểm O bất kì thuộc cạnh a của góc nhị diện [P, a, Q], vẽ các tia Ox, Oy tương ứng thuộc (P), (Q) và vuông góc với a. Góc xOy được gọi là một góc phẳng của góc nhị diện [P, a, Q].
Lời giải chi tiết:
a) Xét tam giác ABC có AB = AC => tam giác ABC cân tại A mà M là trung điểm BC
=> \(AM \bot BC\) (1)
\(\begin{array}{l}SA \bot BC\left( {SA \bot \left( {ABCD} \right)} \right)\\ \Rightarrow BC \bot \left( {SAM} \right);SM \subset \left( {SAM} \right) \Rightarrow BC \bot SM\,\,\,\left( 2 \right)\end{array}\)
Từ (1), (2) ta có \(\widehat {SMA}\) là một góc phẳng của góc nhị diện [S, BC, A].
b) Xét tam giác ABC cân tại A có
\(\widehat {BAC} = {120^0} \Rightarrow \widehat {ACB} = {30^0}\)
\(\sin \widehat {ACB} = \frac{{AM}}{{AC}} \Leftrightarrow \sin {30^0} = \frac{{AM}}{a} \Leftrightarrow AM = \frac{a}{{2 }}\)
\(\tan \widehat {SMA} = \frac{{SA}}{{AM}} = \frac{a}{{2\sqrt 3 }}:\frac{a}{{2 }} = \frac{\sqrt 3}{3} \Rightarrow \widehat {SMA} = 30^0\)
VD1
Video hướng dẫn giải
Trong cửa sổ ở Hình 7.56, cánh và khung cửa là các nửa hình tròn có đường kính 80 cm, bản lề được đính ở điểm chính giữa O của các cung tròn khung và cánh cửa. Khi cửa mở, đường kính của khung và đường kính của cánh song song với nhau và cách nhau một khoảng d; khi cửa đóng, hai đường kính đó trùng nhau. Hãy tính số đo của góc nhị diện có hai nửa mặt phẳng tương ứng chứa cánh, khung cửa khi d = 40 cm.

Phương pháp giải:
Từ một điểm O bất kì thuộc cạnh a của góc nhị diện [P, a, Q], vẽ các tia Ox, Oy tương ứng thuộc (P), (Q) và vuông góc với a. Góc xOy được gọi là một góc phẳng của góc nhị diện [P, a, Q].
Lời giải chi tiết:
Gọi đường kính của khung là AB có tâm I và đường kính của cánh là MN có tâm I’
=> II’ = d = 40cm
Vì đường kính của khung và đường kính của cánh song song với nhau nên mặt phẳng chứa cánh song song với mặt phẳng chứa khung
=> Hai mặt phẳng đó cắt nhau tại 1 đường thẳng d’ qua O song song với AB và MN.
Vì O là điểm chính giữa nên \(OI \bot AB,OI' \bot MN\)
=> \(d' \bot OI,d' \bot OI'\)
Do đó góc nhị diện có hai nửa mặt phẳng tương ứng chứa cánh, khung cửa là góc \(\widehat {IOI'}\)
Xét tam giác IOI’ có
\(OI = OI' = \frac{{80}}{2} = 40 \Rightarrow OI = OI' = II'\)
\( \Rightarrow \) Tam giác IOI’ đều \( \Rightarrow \) \(\widehat {IOI'} = {60^0}\)
Vậy số đo của góc nhị diện có hai nửa mặt phẳng tương ứng chứa cánh, khung cửa khi d = 40 cm là 600
Giải mục 4 trang 47, 48 SGK Toán 11 tập 2 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 4 trang 47, 48 SGK Toán 11 tập 2 - Kết nối tri thức tập trung vào việc ôn tập chương 3: Hàm số lượng giác và ứng dụng của hàm số lượng giác. Đây là một phần quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững các kiến thức về hàm số lượng giác, đồ thị hàm số, phương trình lượng giác và ứng dụng của chúng vào giải quyết các bài toán thực tế.
Nội dung chính của Mục 4
- Ôn tập lý thuyết: Nhắc lại các định nghĩa, tính chất, công thức liên quan đến hàm số lượng giác (sin, cos, tan, cot), các phép biến đổi lượng giác, và các phương pháp giải phương trình lượng giác cơ bản.
- Bài tập trắc nghiệm: Các câu hỏi trắc nghiệm giúp học sinh kiểm tra mức độ hiểu bài và rèn luyện kỹ năng làm bài nhanh.
- Bài tập tự luận: Các bài tập tự luận yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán cụ thể, từ đó củng cố và nâng cao khả năng tư duy logic và giải quyết vấn đề.
Hướng dẫn giải chi tiết các bài tập
Bài 1: (Trang 47)
Bài 1 yêu cầu học sinh xác định tập xác định của hàm số. Để giải bài này, cần nhớ lại điều kiện xác định của các hàm số lượng giác. Ví dụ, hàm số y = tan(x) xác định khi cos(x) ≠ 0.
Bài 2: (Trang 47)
Bài 2 thường liên quan đến việc xét tính chẵn lẻ của hàm số. Học sinh cần nhớ lại định nghĩa về hàm số chẵn, hàm số lẻ và cách kiểm tra tính chẵn lẻ của hàm số.
Bài 3: (Trang 48)
Bài 3 có thể yêu cầu học sinh vẽ đồ thị hàm số hoặc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Để giải bài này, cần nắm vững các phương pháp vẽ đồ thị hàm số và sử dụng các kỹ thuật tìm cực trị của hàm số.
Phương pháp giải bài tập hiệu quả
- Đọc kỹ đề bài: Hiểu rõ yêu cầu của bài toán và các dữ kiện đã cho.
- Xác định kiến thức cần sử dụng: Xác định các định nghĩa, tính chất, công thức liên quan đến bài toán.
- Lập kế hoạch giải: Xác định các bước cần thực hiện để giải bài toán.
- Thực hiện giải: Thực hiện các bước giải theo kế hoạch đã lập.
- Kiểm tra lại kết quả: Đảm bảo kết quả giải đúng và hợp lý.
Lưu ý quan trọng
Khi giải các bài tập về hàm số lượng giác, cần chú ý đến đơn vị đo góc (độ hoặc radian) và các phép biến đổi lượng giác. Ngoài ra, cần rèn luyện kỹ năng vẽ đồ thị hàm số và sử dụng máy tính bỏ túi để tính toán nhanh và chính xác.
Tusach.vn - Đồng hành cùng bạn học Toán 11
Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho tất cả các bài tập trong SGK Toán 11 tập 2 - Kết nối tri thức. Chúng tôi hy vọng rằng những tài liệu này sẽ giúp các em học sinh học tập hiệu quả và đạt kết quả tốt nhất. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Chương | Bài | Link |
|---|---|---|
| 1 | 1 | Link bài 1 |
| 1 | 2 | Link bài 2 |