Lý Thuyết Hàm Số Mũ & Logarit - Toán 11 Kết Nối Tri Thức

Lý thuyết Hàm số mũ và hàm số lôgarit - Toán 11 Kết nối tri thức

Lý Thuyết Hàm Số Mũ và Hàm Số Logarit - Toán 11 Kết Nối Tri Thức

Chào mừng bạn đến với chuyên mục lý thuyết hàm số mũ và hàm số logarit lớp 11 chương trình Kết Nối Tri Thức tại tusach.vn.

Đây là một trong những chủ đề quan trọng của chương trình Toán 11, đóng vai trò nền tảng cho các kiến thức nâng cao hơn.

1. Hàm số mũ a) Khái niệm hàm số mũ

1. Hàm số mũ

a) Khái niệm hàm số mũ

Cho a là số thực dương khác 1.

Hàm số \(y = {a^x}\) được gọi là hàm số mũ cơ số a.

b) Đồ thị và tính chất của hàm số mũ

Hàm số mũ \(y = {a^x}\):

- Có tập xác định là \(\mathbb{R}\) và tập giá trị là \(\left( {0; + \infty } \right)\);

- Đồng biến trên \(\mathbb{R}\) khi a > 1 và nghịch biến trên \(\mathbb{R}\) khi 0 < a < 1;

- Liên tục trên \(\mathbb{R}\);

- Có đồ thị đi qua các điểm (0; 1), (1; a) và luôn nằm phía trên trục hoành.

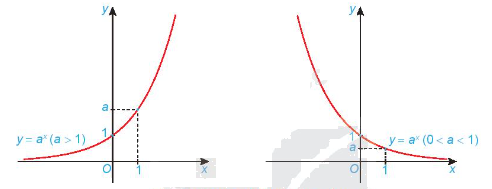
Lý thuyết Hàm số mũ và hàm số lôgarit - Toán 11 Kết nối tri thức 1

Dạng đồ thị của hàm số \(y = {a^x}\)

2. Hàm số lôgarit

a) Khái niệm hàm số lôgarit

Cho a là số thực dương khác 1.

Hàm số \(y = {\log _a}x\) được gọi là hàm số lôgarit cơ số a.

b) Đồ thị và tính chất của hàm số lôgarit

Hàm số lôgarit \(y = {\log _a}x\):

- Có tập xác định là \(\left( {0; + \infty } \right)\) và tập giá trị là \(\mathbb{R}\);

- Đồng biến trên \(\left( {0; + \infty } \right)\) khi a > 1 và nghịch biến trên \(\left( {0; + \infty } \right)\) khi 0 < a < 1;

- Có đồ thị đi qua các điểm (1; 0), (a; 1) và luôn nằm bên phải trục tung.

Lý thuyết Hàm số mũ và hàm số lôgarit - Toán 11 Kết nối tri thức 2

Dạng đồ thị của hàm số \(y = {\log _a}x\)

Lý thuyết Hàm số mũ và hàm số lôgarit - Toán 11 Kết nối tri thức 3

Lý Thuyết Hàm Số Mũ và Hàm Số Logarit - Toán 11 Kết Nối Tri Thức: Tổng Quan

Hàm số mũ và hàm số logarit là hai loại hàm số đặc biệt, đóng vai trò quan trọng trong nhiều lĩnh vực khoa học và kỹ thuật. Trong chương trình Toán 11 Kết Nối Tri Thức, việc nắm vững lý thuyết và các tính chất của hai hàm số này là vô cùng cần thiết để giải quyết các bài toán và xây dựng nền tảng vững chắc cho các kiến thức tiếp theo.

1. Hàm Số Mũ

1.1. Định Nghĩa

Hàm số mũ là hàm số có dạng y = a^x, trong đó:

a là một số thực dương khác 1 (a > 0 và a ≠ 1) gọi là cơ số.
x là biến số thực.

1.2. Tập Xác Định và Tập Giá Trị

Tập xác định của hàm số mũ y = a^x là tập số thực ℝ. Tập giá trị của hàm số mũ là khoảng (0, +∞).

1.3. Tính Chất của Hàm Số Mũ

Hàm số mũ luôn đồng biến nếu a > 1 và nghịch biến nếu 0 < a < 1.
Đồ thị hàm số mũ luôn đi qua điểm (0, 1).
Hàm số mũ không có tiệm cận ngang và tiệm cận đứng.

1.4. Ví Dụ

Ví dụ: y = 2^x là một hàm số mũ với cơ số a = 2.

2. Hàm Số Logarit

2.1. Định Nghĩa

Hàm số logarit là hàm số nghịch đảo của hàm số mũ. Hàm số logarit có dạng y = log_ax, trong đó:

a là một số thực dương khác 1 (a > 0 và a ≠ 1) gọi là cơ số.
x là một số thực dương (x > 0).

2.2. Tập Xác Định và Tập Giá Trị

Tập xác định của hàm số logarit y = log_ax là khoảng (0, +∞). Tập giá trị của hàm số logarit là tập số thực ℝ.

2.3. Tính Chất của Hàm Số Logarit

Hàm số logarit đồng biến nếu a > 1 và nghịch biến nếu 0 < a < 1.
Đồ thị hàm số logarit luôn đi qua điểm (1, 0).
Hàm số logarit có tiệm cận đứng là x = 0.

2.4. Ví Dụ

Ví dụ: y = log₃x là một hàm số logarit với cơ số a = 3.

3. Mối Quan Hệ Giữa Hàm Số Mũ và Hàm Số Logarit

Hàm số mũ và hàm số logarit có mối quan hệ mật thiết với nhau. Cụ thể:

log_a(a^x) = x
a^log_ax = x

4. Bài Tập Vận Dụng

Để củng cố kiến thức về hàm số mũ và hàm số logarit, bạn có thể thực hành giải các bài tập sau:

Giải phương trình: 2^x = 8
Tính giá trị của log₂16
Vẽ đồ thị hàm số y = 3^x

5. Kết Luận

Lý thuyết hàm số mũ và hàm số logarit là một phần quan trọng của chương trình Toán 11 Kết Nối Tri Thức. Việc nắm vững các định nghĩa, tính chất và mối quan hệ giữa hai hàm số này sẽ giúp bạn giải quyết các bài toán một cách hiệu quả và xây dựng nền tảng vững chắc cho các kiến thức nâng cao hơn. Hãy luyện tập thường xuyên và tìm kiếm sự hỗ trợ từ giáo viên hoặc các nguồn tài liệu uy tín để đạt được kết quả tốt nhất.