Giải mục 3 trang 25, 26 SGK Toán 11 tập 1 - Kết nối tri thức

Cho hàm số \(y = \sin x\).

a) Xét tính chẵn, lẻ của hàm số

b) Hoàn thành bảng giá trị sau của hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) bằng cách tính giá trị của \(\sin x\) với những x không âm, sau đó sử dụng kết quả câu a để suy ra giá trị tương ứng của \(\sin x\) với những x âm.

Bằng cách lấy nhiều điểm \(M\left( {x;\sin x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\).

c) Bằng cách làm tương tự câu b cho các đoạn khác có độ dài bằng chu kỳ \(T = 2\pi \), ta được đồ thị của hàm số \(y = \sin x\) như hình dưới đây.

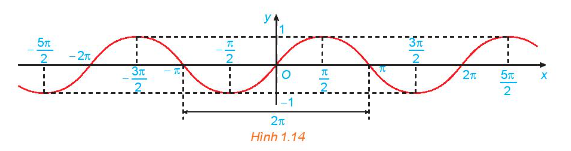
Từ đồ thị ở Hình 1.14, hãy cho biết tập giá trị, các khoảng đồng biến, các khoảng nghịch biến của hàm số \(y = \sin x\)

Phương pháp giải:

Sử dụng định nghĩa hàm số chẵn lẻ

Dựa vào đồ thị để xác định tập giá trị, các khoảng đồng biến, nghịch biến của hàm số.

Lời giải chi tiết:

a) Tập xác định của hàm số là \(D = \mathbb{R}\)

Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D

Ta có: \(f\left( { - x} \right) = \sin \left( { - x} \right) = - \sin x = - f\left( x \right),\;\forall x\; \in \;D\)

Vậy \(y = \sin x\) là hàm số lẻ.

b)

c) Từ đồ thị trên, ta thấy hàm số \(y = \sin x\) có tập xác định là \(\mathbb{R}\), tập giá trị là [-1;1] và đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right),\;k\; \in \;\mathbb{Z}.\)

Tìm tập giá trị của hàm số \(y = 2\sin x\).

Phương pháp giải:

Tập giá trị của hàm số là tập min – max của hàm số trên tập xác định

Lời giải chi tiết:

Tập xác định của hàm số là \(D = \mathbb{R}\)

Vì

\( \Rightarrow \) Tập giá trị của hàm số \(y = 2\sin x\) là \(T = \left[ { - 2;2} \right]\).

Xét tình huống mở đầu.

a) Giải bài toán ở tình huống mở đầu

b) Biết rằng quá trình hít vào xảy ra khi v > 0 và quá trình thở ra khi v < 0. Trong khoảng thời gian từ 0 đến 5 giây, khoảng thời điểm nào thì người đó hít vào? Người đó thở ra?

Phương pháp giải:

Áp dụng công thức tính chu kỳ

Lời giải chi tiết:

a) Chu ký hô hấp: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{\frac{\pi }{3}}} = 6\left( s \right)\)

Số chu kỳ hô hấp trong 1 phút là \(\frac{60}{6}=10\)(chu kì).

b) Ta có: \(v=0,85\sin \frac{\pi t}{3}\)

+) v > 0 khi \(0,85\sin \frac{\pi t}{3}>0\Leftrightarrow \sin \frac{\pi t}{3}>0\)

Mà – 1 ≤ \(\frac{\pi t}{3}\)≤ 1 với mọi x ∈ ℝ. Do đó, \(0<\sin \frac{\pi t}{3}\le 1\).

+) v < 0 khi \(0,85\sin \frac{\pi t}{3}<0\Leftrightarrow \sin \frac{\pi t}{3}<0\).

Mà – 1 ≤ \(\frac{\pi t}{3}\)≤ 1 với mọi x ∈ ℝ. Do đó, −1 ≤ sin\(\frac{\pi t}{3}\) < 0.

+) Với t ∈ (0; 3) ta có 0 < sin\(\frac{\pi t}{3}\) ≤ 1.

+) Với t ∈ (3; 5] ta có −1 ≤ sin\(\frac{\pi t}{3}\) < 0.

Vậy trong khoảng thời gian từ 0 đến 5 giây, khoảng thời điểm sau 0 giây đến trước 3 giây thì người đó hít vào và khoảng thời điểm sau 3 giây đến 5 giây thì người đó thở ra.