Lý thuyết Đường thẳng vuông góc với mặt phẳng - Toán 11 Kết nối tri thức
Tổng quan nội dung
Lý thuyết Đường thẳng vuông góc với mặt phẳng - Toán 11 Kết nối tri thức
Bài học này cung cấp kiến thức nền tảng về điều kiện để một đường thẳng vuông góc với một mặt phẳng trong không gian.
Chúng ta sẽ cùng tìm hiểu các định nghĩa, tính chất quan trọng và phương pháp chứng minh đường thẳng vuông góc với mặt phẳng.
Nội dung được trình bày chi tiết, dễ hiểu, kèm theo ví dụ minh họa giúp học sinh nắm vững lý thuyết và áp dụng vào giải bài tập.
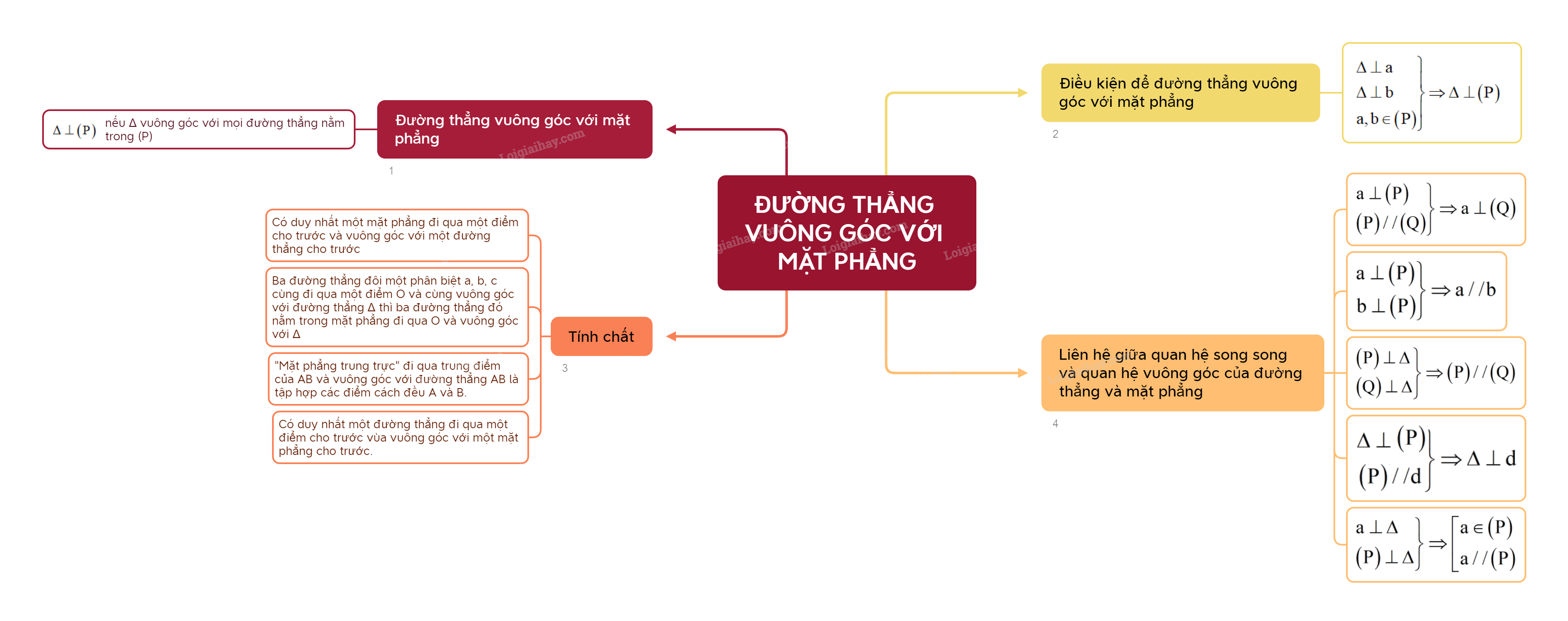
1. Đường thẳng vuông góc với mặt phẳng
1. Đường thẳng vuông góc với mặt phẳng
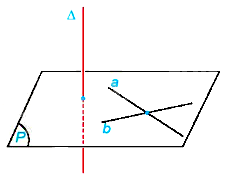
Đường thẳng \(\Delta \) được gọi là vuông góc với mặt phẳng (P) nếu \(\Delta \) vuông góc với mọi đường thẳng nằm trong (P).
Chú ý: Khi \(\Delta \) vuông góc với (P), ta còn nói (P) vuông góc với \(\Delta \) hoặc \(\Delta \) và (P) vuông góc với nhau, kí hiệu \(\Delta \bot \left( P \right)\).
2. Điều kiện để đường thẳng vuông góc với mặt phẳng
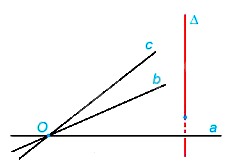
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.
3. Tính chất
- Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
Nhận xét: Nếu ba đường thẳng đôi một phân biệt a, b, c cùng đi qua một điểm O và cùng vuông góc với một đường thẳng \(\Delta \) thì ba đường thẳng đó cùng nằm trong mặt phẳng đi qua O và vuông góc với \(\Delta \).
Chú ý: Mặt phẳng đi qua trung điểm của đoạn thẳng AB và vuông góc với đường thẳng AB được gọi là mặt phẳng trung trực của đoạn thẳng AB. Mặt phẳng trung trực của đoạn thẳng AB là tập hợp các điểm cách đều hai điểm A, B.
- Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
4. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng
- Nếu đường thẳng a vuông góc với mặt phẳng (P) và mặt phẳng (P) song song với mặt phẳng (Q) thì a vuông góc với (Q).
- Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
- Nếu đường thẳng \(\Delta \) vuông góc với mặt phẳng (P) thì \(\Delta \) cũng vuông góc với các mặt phẳng song song với (P).
- Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
- Nếu đường thẳng \(\Delta \) vuông góc với mặt phẳng (P) thì \(\Delta \) vuông góc với mọi đường thẳng song song với (P).
- Nếu đường thẳng a và mặt phẳng (P) cùng vuông góc với một đường thẳng \(\Delta \) thì a nằm trong (P) hoặc song song với (P).
Lý Thuyết Đường Thẳng Vuông Góc Với Mặt Phẳng - Toán 11 Kết Nối Tri Thức
Chào mừng các em học sinh lớp 11 đến với bài học về lý thuyết đường thẳng vuông góc với mặt phẳng, thuộc chương trình Toán 11 Kết nối tri thức. Đây là một trong những kiến thức quan trọng và thường xuyên xuất hiện trong các bài kiểm tra, thi cử. Bài viết này sẽ cung cấp cho các em một cái nhìn tổng quan và chi tiết về chủ đề này.
1. Định nghĩa và Điều kiện Đường Thẳng Vuông Góc Với Mặt Phẳng
Một đường thẳng được gọi là vuông góc với một mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó. Để chứng minh một đường thẳng (d) vuông góc với mặt phẳng (P), ta cần chứng minh (d) vuông góc với hai đường thẳng bất kỳ trong (P) cắt nhau tại một điểm.
- Điều kiện cần: Nếu đường thẳng d vuông góc với mặt phẳng (P) thì d vuông góc với mọi đường thẳng nằm trong (P).
- Điều kiện đủ: Nếu đường thẳng d vuông góc với hai đường thẳng bất kỳ trong (P) cắt nhau tại một điểm thì d vuông góc với mặt phẳng (P).
2. Tính Chất Quan Trọng
Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước.
3. Vectơ Pháp Tuyến của Mặt Phẳng
Một vectơ được gọi là vectơ pháp tuyến của mặt phẳng (P) nếu vectơ đó vuông góc với mọi vectơ nằm trong mặt phẳng (P). Nếu mặt phẳng (P) có phương trình là Ax + By + Cz + D = 0, thì vectơ n = (A; B; C) là một vectơ pháp tuyến của (P).
4. Mối Quan Hệ Giữa Đường Thẳng và Mặt Phẳng
Xét đường thẳng (d) có vectơ chỉ phương u và mặt phẳng (P) có vectơ pháp tuyến n. Ta có:
- (d) vuông góc với (P) khi và chỉ khi u.n = 0 (tích vô hướng của u và n bằng 0).
- (d) song song với (P) khi và chỉ khi u.n = 0 và (d) không có điểm chung với (P).
- (d) cắt (P) khi và chỉ khi u.n ≠ 0.
5. Bài Tập Minh Họa
Bài 1: Cho đường thẳng (d) có phương trình tham số: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P) có phương trình: 2x - y + z - 5 = 0. Chứng minh rằng (d) vuông góc với (P).
Giải:
- Vectơ chỉ phương của (d) là u = (1; -1; 2).
- Vectơ pháp tuyến của (P) là n = (2; -1; 1).
- Tính tích vô hướng u.n = 1*2 + (-1)*(-1) + 2*1 = 2 + 1 + 2 = 5 ≠ 0.
- Vậy (d) không vuông góc với (P). (Đề bài có thể có lỗi)
6. Lời Khuyên Khi Học Lý Thuyết
- Nắm vững định nghĩa và các điều kiện liên quan đến đường thẳng vuông góc với mặt phẳng.
- Hiểu rõ vai trò của vectơ pháp tuyến trong việc xác định tính vuông góc.
- Luyện tập nhiều bài tập để làm quen với các dạng bài khác nhau.
- Sử dụng hình vẽ để minh họa và trực quan hóa các khái niệm.
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về lý thuyết đường thẳng vuông góc với mặt phẳng trong chương trình Toán 11 Kết nối tri thức. Chúc các em học tập tốt!