Giải Mục 3 Trang 74, 75 SGK Toán 11 Tập 1 - Kết Nối Tri Thức
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 11 Tập 1 - Kết Nối Tri Thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tốt nhất để giúp bạn học tập hiệu quả.
Bài viết này sẽ tập trung vào việc giải Mục 3 trang 74, 75, giúp bạn hiểu rõ các khái niệm và phương pháp giải quyết các bài toán liên quan.
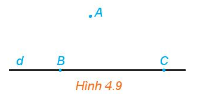
Cho đường thẳng d và điểm A không thuộc d. Trên đường thẳng d lấy hai điểm phân biệt B, C (H.4.9). Mặt phẳng (ABC) có chứa điểm A và đường thẳng d hay không? Mặt phẳng (ABC) có chứa hai đường thẳng AB và BC hay không?
Giải Mục 3 Trang 74, 75 SGK Toán 11 Tập 1 - Kết Nối Tri Thức: Tổng Quan và Phương Pháp Giải
Mục 3 trong SGK Toán 11 Tập 1 - Kết Nối Tri Thức thường xoay quanh các chủ đề về hàm số bậc hai, bao gồm việc xác định các yếu tố của hàm số, vẽ đồ thị, tìm tập xác định, tập giá trị, và giải các bài toán liên quan đến ứng dụng của hàm số bậc hai trong thực tế.
Nội Dung Chính của Mục 3
- Định nghĩa hàm số bậc hai: Hàm số bậc hai có dạng y = ax² + bx + c, với a ≠ 0.
- Hệ số a và tính chất của đồ thị: Hệ số a quyết định độ lồi hoặc lõm của đồ thị. Nếu a > 0, đồ thị có dạng parabol mở lên trên; nếu a < 0, đồ thị có dạng parabol mở xuống dưới.
- Đỉnh của parabol: Tọa độ đỉnh của parabol là I(x₀; y₀), với x₀ = -b/2a và y₀ = f(x₀).
- Trục đối xứng của parabol: Trục đối xứng của parabol là đường thẳng x = x₀.
- Tìm tập xác định và tập giá trị của hàm số: Tập xác định của hàm số bậc hai là R. Tập giá trị phụ thuộc vào dấu của hệ số a.
Hướng Dẫn Giải Bài Tập Trang 74, 75
Để giải các bài tập trong Mục 3 trang 74, 75, bạn cần nắm vững các kiến thức cơ bản về hàm số bậc hai và áp dụng các công thức, phương pháp đã học. Dưới đây là một số gợi ý:
- Xác định các yếu tố của hàm số: Xác định hệ số a, b, c, đỉnh, trục đối xứng, và tập xác định, tập giá trị của hàm số.
- Vẽ đồ thị hàm số: Sử dụng các yếu tố đã xác định để vẽ đồ thị hàm số.
- Giải các phương trình, bất phương trình liên quan đến hàm số: Sử dụng các phương pháp giải phương trình, bất phương trình bậc hai để tìm nghiệm.
- Ứng dụng hàm số bậc hai vào giải quyết các bài toán thực tế: Phân tích bài toán, xây dựng mô hình toán học, và giải quyết bài toán bằng cách sử dụng hàm số bậc hai.
Ví dụ Minh Họa
Bài 1: Cho hàm số y = 2x² - 4x + 1. Tìm đỉnh và trục đối xứng của parabol.
Giải:
- Hệ số a = 2, b = -4, c = 1.
- Tọa độ đỉnh: x₀ = -b/2a = -(-4)/(2*2) = 1; y₀ = 2(1)² - 4(1) + 1 = -1. Vậy đỉnh của parabol là I(1; -1).
- Trục đối xứng: x = 1.
Lưu Ý Quan Trọng
Khi giải các bài tập về hàm số bậc hai, bạn cần chú ý đến các điều kiện của bài toán, lựa chọn phương pháp giải phù hợp, và kiểm tra lại kết quả để đảm bảo tính chính xác.
Bảng Tổng Hợp Công Thức Quan Trọng
| Công Thức | Mô Tả |
|---|
| x₀ = -b/2a | Hoành độ đỉnh của parabol |
| y₀ = f(x₀) | Tung độ đỉnh của parabol |
| Δ = b² - 4ac | Biệt thức của phương trình bậc hai |
Hy vọng với những hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong việc giải các bài tập Mục 3 trang 74, 75 SGK Toán 11 Tập 1 - Kết Nối Tri Thức. Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại liên hệ với chúng tôi tại tusach.vn!
