Giải mục 6 trang 29, 30 SGK Toán 11 tập 1 - Kết nối tri thức

Tusach.vn xin giới thiệu lời giải chi tiết mục 6 trang 29, 30 SGK Toán 11 tập 1 - Kết nối tri thức. Bài viết này sẽ giúp các em học sinh hiểu rõ hơn về nội dung bài học và tự tin giải các bài tập liên quan.

Chúng tôi cung cấp đáp án chính xác, dễ hiểu, kèm theo các bước giải chi tiết và lời giải thích rõ ràng.

Cho hàm số \(y = \cot x\) a) Xét tính chẵn, lẻ của hàm số

Hoạt động 7

Cho hàm số \(y = \cot x\)

a) Xét tính chẵn, lẻ của hàm số

b) Hoàn thành bảng giá trị của hàm số \(y = \cot x\) trên khoảng\(\;\left( {0;\pi } \right)\).

\(x\)	\(\frac{\pi }{6}\)	\(\frac{\pi }{4}\)	\(\frac{\pi }{3}\)	\(\frac{\pi }{2}\)	\(\frac{{2\pi }}{3}\)	\(\frac{{3\pi }}{4}\)	\(\frac{{5\pi }}{6}\)
\(y = \cot x\)	?	?	?	?	?	?	?

Bằng cách lấy nhiều điểm \(M\left( {x;\cot x} \right)\) với \(x \in \left( {0;\pi } \right)\) và nối lại ta được đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\).

c) Bằng cách làm tương tự câu b cho các đoạn khác có độ dài bằng chu kỳ \(T = \pi \), ta được đồ thị của hàm số \(y = \cot x\) như hình dưới đây.

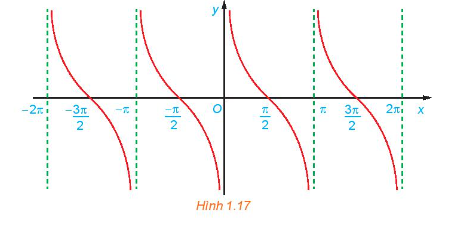
Giải mục 6 trang 29, 30 SGK Toán 11 tập 1 - Kết nối tri thức 1

Từ đồ thị ở Hình 1.17, hãy tìm tập giá trị và các khoảng nghịch biến của hàm số \(y = \cot x\)

Phương pháp giải:

Sử dụng định nghĩa hàm số chẵn lẻ

Dựa vào đồ thị để xác định tập giá trị, các khoảng đồng biến, nghịch biến của hàm số.

Lời giải chi tiết:

a) Tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ {k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\)

Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D

Ta có: \(f\left( { - x} \right) = \cot \left( { - x} \right) = - \cot x = - f\left( x \right),\;\forall x\; \in \;D\)

Vậy \(y = \cot x\) là hàm số lẻ.

\(x\)	\(\frac{\pi }{6}\)	\(\frac{\pi }{4}\)	\(\frac{\pi }{3}\)	\(\frac{\pi }{2}\)	\(\frac{{2\pi }}{3}\)	\(\frac{{3\pi }}{4}\)	\(\frac{{5\pi }}{6}\)
\(\cot x\)	\(\sqrt 3 \)	\(1\)	\(\frac{{\sqrt 3 }}{3}\)	\(0\)	\( - \frac{{\sqrt 3 }}{3}\)	\( - 1\)	\( - \sqrt 3 \)

c) Từ đồ thị trên, ta thấy hàm số \(y = \cot x\) có tập xác định là \(\mathbb{R}\backslash \left\{ {k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\), tập giá trị là \(\mathbb{R}\) và nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right)\).

Luyện tập

Sử dụng đồ thị đã vẽ ở Hình 1.17, hãy xác định các giá trị của x trên đoạn \(\left[ { - \frac{\pi }{2};2\pi } \right]\) để hàm số \(y = \cot x\) nhận giá trị dương.

Phương pháp giải:

Nhìn đồ thị để xác định vị trí của y và x

Lời giải chi tiết:

Hàm số nhận giá trị dương ứng với phần đồ thị nằm trên trục hoành. Từ đồ thị ta suy ra trên đoạn \(\left[ { - \frac{\pi }{2};2\pi } \right]\), thì \(y > 0\) khi \(x\; \in \left( {0;\frac{\pi }{2}} \right) \cup \left( {\;\pi ;\frac{{3\pi }}{2}} \right)\)

Giải mục 6 trang 29, 30 SGK Toán 11 tập 1 - Kết nối tri thức: Tổng quan và Phương pháp giải

Mục 6 trang 29, 30 SGK Toán 11 tập 1 - Kết nối tri thức tập trung vào việc ôn tập chương 1: Hàm số và đồ thị. Đây là một phần quan trọng trong chương trình Toán 11, đặt nền móng cho các kiến thức tiếp theo. Việc nắm vững các khái niệm và phương pháp giải bài tập trong mục này là vô cùng cần thiết.

Nội dung chính của Mục 6

Ôn tập về hàm số: Các loại hàm số (hàm số bậc nhất, hàm số bậc hai, hàm số mũ, hàm số logarit), tập xác định, tập giá trị, tính đơn điệu, cực trị.
Đồ thị hàm số: Cách vẽ đồ thị hàm số, các điểm đặc biệt trên đồ thị (điểm cực trị, điểm uốn, giao điểm với các trục tọa độ).
Ứng dụng của hàm số: Giải các bài toán thực tế liên quan đến hàm số.

Các dạng bài tập thường gặp

Xác định tập xác định của hàm số: Yêu cầu học sinh phải nắm vững điều kiện xác định của các loại hàm số khác nhau.
Tìm tập giá trị của hàm số: Sử dụng các phương pháp như xét hàm số trên một khoảng, sử dụng đạo hàm để tìm cực trị.
Khảo sát hàm số: Xác định tính đơn điệu, cực trị, điểm uốn của hàm số.
Vẽ đồ thị hàm số: Sử dụng các điểm đặc biệt và tính chất của hàm số để vẽ đồ thị.
Giải phương trình, bất phương trình: Sử dụng đồ thị hàm số hoặc các phương pháp đại số để giải.

Hướng dẫn giải chi tiết các bài tập trong Mục 6

Dưới đây là hướng dẫn giải chi tiết một số bài tập tiêu biểu trong Mục 6 trang 29, 30 SGK Toán 11 tập 1 - Kết nối tri thức:

Bài 1: (Trang 29)

Đề bài: Xác định tập xác định của hàm số f(x) = √(x - 2) + 1/(x + 1).

Lời giải:

Điều kiện xác định của √(x - 2) là x - 2 ≥ 0 ⇔ x ≥ 2.
Điều kiện xác định của 1/(x + 1) là x + 1 ≠ 0 ⇔ x ≠ -1.
Kết hợp hai điều kiện trên, ta được tập xác định của hàm số là [2, +∞).

Bài 2: (Trang 30)

Đề bài: Tìm tập giá trị của hàm số y = x² - 4x + 3.

Lời giải:

Hàm số y = x² - 4x + 3 là một hàm số bậc hai có a = 1 > 0. Do đó, hàm số có giá trị nhỏ nhất tại đỉnh của parabol.

Hoành độ đỉnh của parabol là x₀ = -b/(2a) = -(-4)/(2*1) = 2.

Giá trị nhỏ nhất của hàm số là y₀ = (2)² - 4(2) + 3 = -1.

Vậy tập giá trị của hàm số là [-1, +∞).

Mẹo học tập hiệu quả

Nắm vững định nghĩa và tính chất của các loại hàm số.
Luyện tập thường xuyên các bài tập về khảo sát hàm số và vẽ đồ thị.
Sử dụng các công cụ hỗ trợ như máy tính cầm tay hoặc phần mềm vẽ đồ thị.
Tìm kiếm sự giúp đỡ từ giáo viên hoặc bạn bè khi gặp khó khăn.

Kết luận

Giải mục 6 trang 29, 30 SGK Toán 11 tập 1 - Kết nối tri thức đòi hỏi sự hiểu biết vững chắc về các kiến thức cơ bản về hàm số và đồ thị. Hy vọng với hướng dẫn chi tiết và các mẹo học tập trên, các em học sinh sẽ tự tin hơn trong việc giải các bài tập và đạt kết quả tốt trong môn Toán.

Giải mục 6 trang 29, 30 SGK Toán 11 tập 1 - Kết nối tri thức

Giải mục 6 trang 29, 30 SGK Toán 11 tập 1 - Kết nối tri thức

Hoạt động 7

Luyện tập

Giải mục 6 trang 29, 30 SGK Toán 11 tập 1 - Kết nối tri thức: Tổng quan và Phương pháp giải

Nội dung chính của Mục 6

Các dạng bài tập thường gặp

Hướng dẫn giải chi tiết các bài tập trong Mục 6

Bài 1: (Trang 29)

Bài 2: (Trang 30)

Mẹo học tập hiệu quả

Kết luận

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN