Giải mục 2 trang 18, 19 SGK Toán 11 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải Mục 2 Trang 18, 19 Toán 11 Tập 2 - Kết Nối Tri Thức
Chào mừng bạn đến với lời giải chi tiết Mục 2 trang 18, 19 SGK Toán 11 tập 2 - Kết Nối Tri Thức trên tusach.vn. Chúng tôi hiểu rằng việc giải các bài tập Toán học đôi khi có thể gặp khó khăn, đặc biệt là với những chủ đề mới.
Bài viết này sẽ cung cấp cho bạn đáp án chính xác, phương pháp giải rõ ràng và những lưu ý quan trọng để bạn có thể tự tin chinh phục các bài tập trong sách giáo khoa.
a) Tính (y = {log _2}x) khi x lần lượt nhận các giá trị 1; 2; 4. Với mỗi giá trị của x > 0 có bao nhiêu giá trị của (y = {log _2}x) tương ứng?
HĐ 3
Video hướng dẫn giải
a) Tính \(y = {\log _2}x\) khi x lần lượt nhận các giá trị 1; 2; 4. Với mỗi giá trị của x > 0 có bao nhiêu giá trị của \(y = {\log _2}x\) tương ứng?
b) Với những giá trị nào của x, biểu thức \(y = {\log _2}x\) có nghĩa?
Phương pháp giải:
Thay các giá trị x lần lượt để tính y.
Lời giải chi tiết:
a) Với \(x = 1\) thì \(y = {\log _2}1 = 0\)
Với \(x = 2\) thì \(y = {\log _2}2 = 1\)
Với \(x = 4\) thì \(y = {\log _2}4 = 2\)
b) Biểu thức \(y = {\log _2}x\) có nghĩa khi x > 0.
CH
Video hướng dẫn giải
Trong các hàm số sau, những hàm số nào là hàm số lôgarit? Khi đó hãy chỉ ra cơ số.
a) \(y = {\log _{\sqrt 3 }}x;\)
b) \(y = {\log _{{2^{ - 2}}}}x;\)
c) \(y = {\log _x}2;\)
d) \(y = {\log _{\frac{1}{x}}}5.\)
Phương pháp giải:
Sử dụng định nghĩa hàm số lôgarit
Lời giải chi tiết:
a) \(y = {\log _{\sqrt 3 }}x\) là hàm số lôgarit có cơ số \(\sqrt 3 .\)
b) \(y = {\log _{{2^{ - 2}}}}x;\) là hàm số lôgarit có cơ số \({2^{ - 2}} = \frac{1}{4}.\)
c) \(y = {\log _x}2\) không là hàm số lôgarit.
d) \(y = {\log _{\frac{1}{x}}}5\) không hàm số lôgarit.
HĐ 4
Video hướng dẫn giải
Cho hàm số lôgarit \(y = {\log _2}x.\)
a) Hoàn thành bảng giá trị sau:

b) Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;{{\log }_2}x} \right)\) với \(x \in \mathbb{R}\) và nối lại ta được đồ thị của hàm số \(y = {\log _2}x\)
c) Từ đồ thị đã vẽ ở câu b, hãy kết luận về tập giá trị và tính chất biến thiên của hàm số \(y = {\log _2}x\)
Phương pháp giải:
Vẽ đồ thị dựa vào các điểm đã lấy sau đó nhìn đồ thị để đưa ra tập giá trị và tính chất biến thiên.
Lời giải chi tiết:
a) Lập bảng giá trị của hàm số tại một điểm như sau:

b,
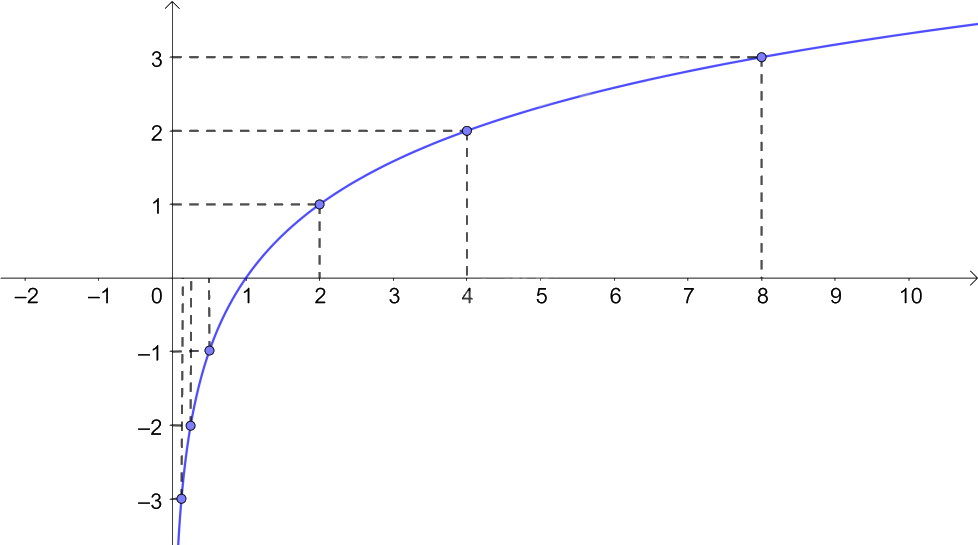
c) Tập giá trị: \(\mathbb{R}\)
Tính chất biến thiên: đồng biến
VD
Video hướng dẫn giải
Giải bài toán tình huống mở đầu (kết quả tính theo đơn vị triệu người và làm tròn đến chữ số thập phân thứ hai).
Sự tăng trưởng dân số ước tính theo công thức tăng trưởng mũ sau:
\(A = P{e^{rt}}\),
trong đó P là dân số của năm lấy làm mốc, A là dân số sau t năm, r là tỉ lệ tăng dân số hằng năm. Biết rằng vào năm 2020, dân số Việt Nam khoảng 97,34 triệu người và tỉ lệ tăng dân số là 0,91% (theo danso.org). Nếu tỉ lệ tăng dân số này giữ nguyên, hãy ước tính dân số Việt Nam vào năm 2050.
Phương pháp giải:
Sử dụng công thức tăng trưởng mũ: \(A = P{e^{rt}}\)
Lời giải chi tiết:
Từ năm 2020 đến năm 2050 là 30 năm.
Ước tính dân số Việt Nam vào năm 2050 là: \(97,34.{e^{0,91\% .30}} = 127,8950498\)(triệu người)
Giải Mục 2 Trang 18, 19 Toán 11 Tập 2 - Kết Nối Tri Thức: Tổng Quan và Phương Pháp Giải
Mục 2 trong SGK Toán 11 tập 2 - Kết Nối Tri Thức tập trung vào các kiến thức về đường thẳng và mặt phẳng trong không gian. Đây là một phần quan trọng, đặt nền móng cho các kiến thức hình học không gian phức tạp hơn ở các lớp trên. Việc nắm vững các khái niệm, định lý và phương pháp giải bài tập trong mục này là vô cùng cần thiết.
Nội Dung Chính của Mục 2
Mục 2 bao gồm các nội dung chính sau:
- Vị trí tương đối của hai đường thẳng trong không gian: Song song, cắt nhau, chéo nhau.
- Góc giữa hai đường thẳng trong không gian: Cách tính góc, các trường hợp đặc biệt.
- Vị trí tương đối của đường thẳng và mặt phẳng trong không gian: Nằm trong mặt phẳng, song song với mặt phẳng, cắt mặt phẳng.
- Góc giữa đường thẳng và mặt phẳng trong không gian: Cách tính góc, các ứng dụng.
Giải Chi Tiết Các Bài Tập Trang 18, 19
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 2 trang 18, 19 SGK Toán 11 tập 2 - Kết Nối Tri Thức:
Bài 1: (Trang 18)
Đề bài: (Giả sử đề bài là xác định vị trí tương đối của hai đường thẳng cho trước)
Lời giải: Để xác định vị trí tương đối của hai đường thẳng, ta cần xét các vectơ chỉ phương của chúng. Nếu hai vectơ chỉ phương cùng phương thì hai đường thẳng song song hoặc trùng nhau. Nếu hai vectơ chỉ phương không cùng phương, ta xét giao điểm của hai đường thẳng. Nếu hai đường thẳng có giao điểm thì chúng cắt nhau. Nếu hai đường thẳng không có giao điểm và không cùng phương thì chúng chéo nhau.
(Giải chi tiết các bước tính toán và kết luận)
Bài 2: (Trang 19)
Đề bài: (Giả sử đề bài là tính góc giữa hai đường thẳng)
Lời giải: Góc giữa hai đường thẳng được tính bằng công thức: cos(α) = |a.b| / (|a||b|), trong đó a và b là các vectơ chỉ phương của hai đường thẳng. Ta cần tìm các vectơ chỉ phương, tính tích vô hướng và độ dài của chúng, sau đó áp dụng công thức để tìm góc α.
(Giải chi tiết các bước tính toán và kết luận)
Bài 3: (Trang 19)
Đề bài: (Giả sử đề bài là xác định góc giữa đường thẳng và mặt phẳng)
Lời giải: Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng. Để tính góc này, ta cần tìm vectơ chỉ phương của đường thẳng và vectơ pháp tuyến của mặt phẳng. Sau đó, áp dụng công thức: sin(α) = |a.n| / (|a||n|), trong đó a là vectơ chỉ phương của đường thẳng và n là vectơ pháp tuyến của mặt phẳng.
(Giải chi tiết các bước tính toán và kết luận)
Mẹo Giải Bài Tập Hiệu Quả
Để giải các bài tập về đường thẳng và mặt phẳng trong không gian một cách hiệu quả, bạn nên:
- Nắm vững các định nghĩa, định lý và công thức liên quan.
- Vẽ hình minh họa để hình dung rõ hơn về bài toán.
- Sử dụng các vectơ để biểu diễn các yếu tố hình học.
- Kiểm tra lại kết quả sau khi giải xong.
Tài Liệu Tham Khảo Thêm
Ngoài SGK, bạn có thể tham khảo thêm các tài liệu sau:
- Sách bài tập Toán 11 tập 2 - Kết Nối Tri Thức
- Các trang web học Toán trực tuyến uy tín
- Các video hướng dẫn giải bài tập Toán 11
Hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về Mục 2 trang 18, 19 SGK Toán 11 tập 2 - Kết Nối Tri Thức và có thể tự tin giải các bài tập liên quan. Chúc bạn học tập tốt!