Lý Thuyết Cấp Số Cộng - Toán 11 Kết Nối Tri Thức

Lý thuyết Cấp số cộng - SGK Toán 11 Kết nối tri thức

Lý thuyết Cấp số cộng - Nền tảng Toán học 11

Cấp số cộng là một trong những khái niệm quan trọng trong chương trình Toán 11, đặc biệt là trong chương trình Kết nối tri thức.

Hiểu rõ lý thuyết về cấp số cộng không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn là nền tảng vững chắc cho các kiến thức toán học nâng cao hơn.

Tusach.vn cung cấp tài liệu học tập đầy đủ và chi tiết về lý thuyết cấp số cộng, giúp bạn nắm vững kiến thức một cách dễ dàng.

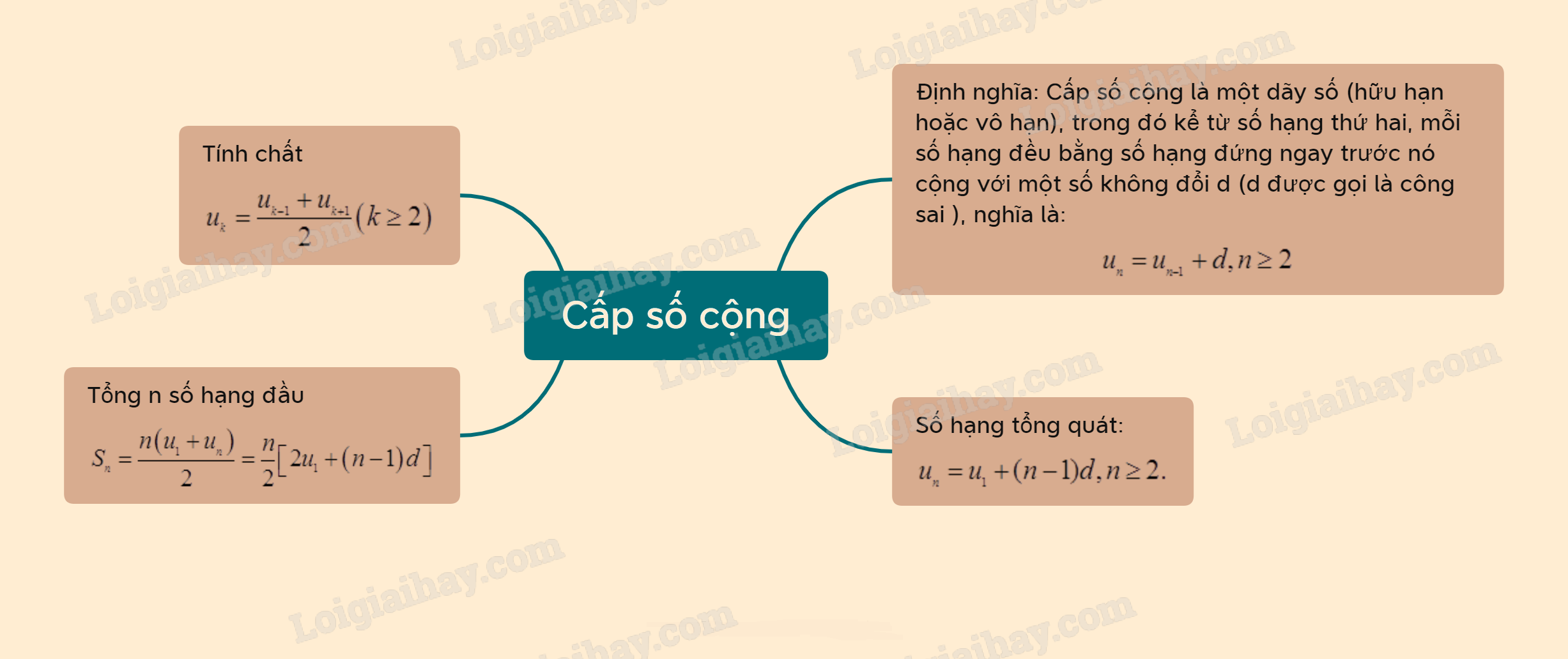
1. Định nghĩa

1. Định nghĩa

Cấp số cộng là một dãy số (hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d. Số d được gọi là công sai của cấp số cộng.

Cấp số cộng \(\left( {{u_n}} \right)\)với công sai d được cho bởi hệ thức truy hồi

\({u_n} = {u_{n - 1}} + d,n \ge 2\)

* Nhận xét: Nếu \(\left( {{u_n}} \right)\) là cấp số cộng thì kể từ số hạng thứ 2, mỗi số hạng (trừ số hạng cuối đối với cấp số cộng hữu hạn) đều là trung bình cộng của 2 sô hạng đứng kề nó trong dãy, tức là:

\({u_k} = \frac{{{u_{k - 1}} + {u_{k + 1}}}}{2}\left( {k \ge 2} \right)\)

2. Số hạng tổng quát

Nếu cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu là \({u_1}\) và công sai d thì số hạng tổng quát \({u_n}\)của nó được xác định theo công thức \({u_n} = {u_1} + (n - 1)d,n \ge 2.\)

3. Tổng n số hạng đầu của một cấp số cộng

Cho cấp số cộng \(\left( {{u_n}} \right)\)với công sai d. Đặt \({S_n} = {u_1} + {u_2} + {u_3} + ... + {u_n}\). Khi đó

\({S_n} = \frac{{n\left( {{u_1} + {u_n}} \right)}}{2} = \frac{n}{2}\left[ {2{u_1} + \left( {n - 1} \right)d} \right]\)

Lý thuyết Cấp số cộng - SGK Toán 11 Kết nối tri thức 1

Lý Thuyết Cấp Số Cộng - SGK Toán 11 Kết Nối Tri Thức: Tổng Quan Chi Tiết

Cấp số cộng là một dãy số mà mỗi số hạng sau được tạo thành bằng cách cộng một số không đổi (gọi là công sai) vào số hạng đứng trước. Đây là một khái niệm cơ bản nhưng vô cùng quan trọng trong chương trình Toán học lớp 11, đặc biệt là theo chương trình Kết nối tri thức. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về lý thuyết cấp số cộng, bao gồm định nghĩa, tính chất, công thức và các ứng dụng thực tế.

1. Định Nghĩa Cấp Số Cộng

Một dãy số (u_n) được gọi là cấp số cộng nếu có một số thực d sao cho:

u_n+1 = u_n + d, với mọi n ≥ 1

Số d được gọi là công sai của cấp số cộng. Nếu d > 0, cấp số cộng là tăng. Nếu d < 0, cấp số cộng là giảm. Nếu d = 0, cấp số cộng là hằng.

2. Các Tính Chất Quan Trọng của Cấp Số Cộng

Một số tính chất quan trọng cần nhớ:

Mọi số hạng của cấp số cộng đều có thể biểu diễn qua số hạng đầu (u₁) và công sai (d): u_n = u₁ + (n-1)d
Tổng của n số hạng đầu tiên của cấp số cộng được tính bằng công thức: S_n = n/2 * (u₁ + u_n) = n/2 * [2u₁ + (n-1)d]
Nếu ba số a, b, c theo thứ tự đó lập thành một cấp số cộng thì 2b = a + c.

3. Công Thức Tính Số Hạng Tổng Quát và Tổng của Cấp Số Cộng

Đây là hai công thức quan trọng nhất cần nắm vững:

Công thức	Mô tả
u_n = u₁ + (n-1)d	Tính số hạng thứ n của cấp số cộng
S_n = n/2 * (u₁ + u_n)	Tính tổng của n số hạng đầu tiên
S_n = n/2 * [2u₁ + (n-1)d]	Tính tổng của n số hạng đầu tiên (khi biết u₁ và d)

4. Ứng Dụng của Cấp Số Cộng trong Thực Tế

Cấp số cộng xuất hiện trong nhiều tình huống thực tế, ví dụ:

Tính số tiền tiết kiệm hàng tháng với lãi suất cố định.
Tính chiều dài các cạnh của một hình vuông hoặc hình chữ nhật khi tăng dần đều.
Mô tả sự tăng trưởng dân số hoặc doanh thu theo thời gian.

5. Bài Tập Vận Dụng (Ví dụ)

Bài 1: Cho cấp số cộng có u₁ = 2 và d = 3. Tính u₅ và S₅.

Giải:

u₅ = u₁ + (5-1)d = 2 + 4*3 = 14
S₅ = 5/2 * (u₁ + u₅) = 5/2 * (2 + 14) = 40

6. Lời Khuyên Khi Học Lý Thuyết Cấp Số Cộng

Để nắm vững lý thuyết cấp số cộng, bạn nên:

Hiểu rõ định nghĩa và các tính chất cơ bản.
Luyện tập giải nhiều bài tập khác nhau để làm quen với các dạng bài.
Sử dụng các công thức một cách linh hoạt và chính xác.
Tìm hiểu các ứng dụng thực tế của cấp số cộng để hiểu rõ hơn về tầm quan trọng của nó.

Tusach.vn hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về lý thuyết cấp số cộng. Chúc bạn học tập tốt!