Giải mục 4 trang 36 SGK Toán 11 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 4 trang 36 SGK Toán 11 tập 1 - Kết nối tri thức
Chào mừng bạn đến với lời giải chi tiết mục 4 trang 36 SGK Toán 11 tập 1 - Kết nối tri thức trên tusach.vn. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và những lưu ý quan trọng để bạn có thể tự tin giải quyết các bài tập tương tự.
a) Quan sát Hình 1.24, hãy cho biết đường thẳng (y = 1) cắt đồ thị hàm số (y = tan x) tại mấy điểm trên khoảng (left( { - frac{pi }{2};frac{pi }{2}} right)?)
HĐ 4
Video hướng dẫn giải
a) Quan sát Hình 1.24, hãy cho biết đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = \tan x\) tại mấy điểm trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)?\)
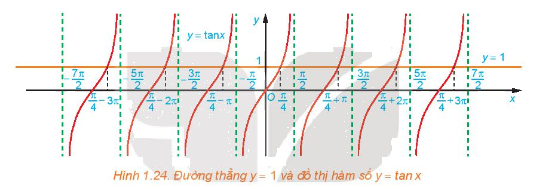
b) Dựa vào tính tuần hoàn của hàm tang, hãy viết công thức nghiệm của phương trình đã cho
Phương pháp giải:
Nghiệm của phương trình \(\tan x = 1\) là hoành độ các giao điểm của đường thẳng \(y = 1\) và đồ thị hàm số \(y = \tan x\)
Lời giải chi tiết:
a) Từ Hình 1.24, ta thấy đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = \tan x\;\)tại 1 điểm \(x = \frac{\pi }{4}\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\)
b) Ta có công thức nghiệm của phương trình là: \(x = \frac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)
LT 4
Video hướng dẫn giải
Giải các phương trình sau:
a) \(\sqrt 3 \tan 2x = - 1\); b) \(\tan 3x + \tan 5x = 0\)’
Phương pháp giải:
Dựa vào công thức nghiệm tổng quát: \(\tan x = m\; \Leftrightarrow \tan x = \tan \alpha \Leftrightarrow x = \alpha + k\pi \;\left( {k \in \mathbb{Z}} \right)\)
Lời giải chi tiết:
a) \(\sqrt 3 \tan 2x = - 1\;\; \Leftrightarrow \tan 2x = - \frac{1}{{\sqrt 3 }}\;\;\; \Leftrightarrow \tan 2x = \tan - \frac{\pi }{6}\; \Leftrightarrow 2x = - \frac{\pi }{6} + k\pi \)
\(\;\; \Leftrightarrow x = - \frac{\pi }{{12}} + \frac{{k\pi }}{2}\;\left( {k \in \mathbb{Z}} \right)\)
b) \(\tan 3x + \tan 5x = 0\;\; \Leftrightarrow \tan 3x = \tan \left( { - 5x} \right) \Leftrightarrow 3x = - 5x + k\pi \;\; \Leftrightarrow 8x = k\pi \;\; \Leftrightarrow x = \frac{{k\pi }}{8}\;\left( {k \in \mathbb{Z}} \right)\)
Giải mục 4 trang 36 SGK Toán 11 tập 1 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 4 trang 36 SGK Toán 11 tập 1 - Kết nối tri thức tập trung vào việc ứng dụng các kiến thức về hàm số bậc hai đã học để giải quyết các bài toán thực tế. Nội dung chính bao gồm việc xác định các yếu tố của hàm số, vẽ đồ thị hàm số và tìm các điểm đặc biệt của đồ thị như đỉnh, trục đối xứng, giao điểm với các trục tọa độ.
Nội dung chi tiết các bài tập trong mục 4
Mục 4 thường bao gồm các bài tập sau:
- Bài 1: Xác định các hệ số a, b, c của hàm số bậc hai.
- Bài 2: Tìm tọa độ đỉnh của parabol.
- Bài 3: Vẽ đồ thị hàm số bậc hai.
- Bài 4: Tìm giao điểm của đồ thị hàm số với trục hoành và trục tung.
- Bài 5: Giải các bài toán ứng dụng liên quan đến hàm số bậc hai (ví dụ: tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số).
Lời giải chi tiết từng bài tập
Bài 1: Xác định hệ số a, b, c
Để xác định hệ số a, b, c của hàm số bậc hai y = ax2 + bx + c, bạn cần đưa hàm số về dạng tổng quát. Ví dụ, nếu hàm số cho là y = 2x2 - 5x + 1, thì a = 2, b = -5, c = 1.
Bài 2: Tìm tọa độ đỉnh của parabol
Tọa độ đỉnh của parabol y = ax2 + bx + c được tính theo công thức:
- xđỉnh = -b / (2a)
- yđỉnh = -Δ / (4a) (với Δ = b2 - 4ac)
Ví dụ, với hàm số y = x2 - 4x + 3, ta có:
- xđỉnh = -(-4) / (2 * 1) = 2
- Δ = (-4)2 - 4 * 1 * 3 = 4
- yđỉnh = -4 / (4 * 1) = -1
Vậy tọa độ đỉnh của parabol là (2, -1).
Bài 3: Vẽ đồ thị hàm số bậc hai
Để vẽ đồ thị hàm số bậc hai, bạn cần thực hiện các bước sau:
- Xác định các yếu tố của hàm số (a, b, c, đỉnh, trục đối xứng, giao điểm với các trục tọa độ).
- Lập bảng giá trị của x và y.
- Vẽ các điểm trên mặt phẳng tọa độ và nối chúng lại để được đồ thị hàm số.
Lưu ý quan trọng khi giải bài tập
- Luôn kiểm tra điều kiện xác định của hàm số.
- Sử dụng đúng công thức và phương pháp giải.
- Kiểm tra lại kết quả sau khi giải xong.
Tusach.vn – Hỗ trợ học tập Toán 11 hiệu quả
Tusach.vn cam kết cung cấp lời giải chi tiết, chính xác và dễ hiểu cho tất cả các bài tập trong SGK Toán 11 tập 1 - Kết nối tri thức. Chúng tôi luôn cập nhật nội dung mới nhất và cung cấp nhiều tài liệu học tập hữu ích khác để giúp bạn học tập hiệu quả hơn. Hãy truy cập tusach.vn ngay hôm nay để khám phá!
| Bài tập | Lời giải |
|---|---|
| Bài 1 | Xem lời giải |
| Bài 2 | Xem lời giải |