Bài 5.6 trang 109 Toán 11 Tập 1 - Kết nối tri thức

Bài 5.6 trang 109 SGK Toán 11 tập 1 - Kết nối tri thức

Bài 5.6 trang 109 SGK Toán 11 Tập 1 - Kết nối tri thức

Bài 5.6 thuộc chương trình Toán 11 Tập 1, sách Kết nối tri thức, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến đạo hàm của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để tìm đạo hàm và giải quyết các vấn đề thực tế.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

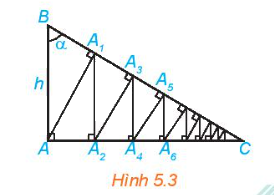
Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng (alpha ) (H.5.3). Từ A kẻ (A{A_1} bot BC), từ ({A_1}) kẻ ({A_1}{A_2} bot AC), sau đó lại kẻ ({A_2}{A_3} bot BC). Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn (A{A_1}{A_2}{A_3} ldots ) Tính độ dài đường gấp khúc này theo h và (alpha )

Đề bài

Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng \(\alpha \) (H.5.3). Từ A kẻ \(A{A_1} \bot BC\), từ \({A_1}\) kẻ \({A_1}{A_2} \bot AC\), sau đó lại kẻ \({A_2}{A_3} \bot BC\). Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn \(A{A_1}{A_2}{A_3} \ldots \) Tính độ dài đường gấp khúc này theo h và \(\alpha \)

Bài 5.6 trang 109 SGK Toán 11 tập 1 - Kết nối tri thức 1

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Bài 5.6 trang 109 SGK Toán 11 tập 1 - Kết nối tri thức 2

Dựa vào đề bài để tìm ra công thức tổng quát.

Lời giải chi tiết

Độ dài đường gấp khúc tạo thành cấp số nhân với số hạng tổng quát là:

\({u_n} = sin\;\alpha \; \times h \times {\left( {sin\;\alpha \;} \right)^{n - 1}}\).

Độ dài đường gập khúc: \(A{A_1} + {A_2}{A_3} + \ldots \).

Đây là tổng cấp số nhân lùi vô hạn với \({u_1} = sin\;\alpha \; \times h,\;q = sin\;\alpha \;\).

Nên \(A{A_1} + {A_2}{A_3} + \ldots = \frac{{sin\;\alpha \; \times h}}{{1 - sin\;\alpha \;}}\).

Bài 5.6 trang 109 SGK Toán 11 Tập 1 - Kết nối tri thức: Giải chi tiết và hướng dẫn

Bài 5.6 trang 109 SGK Toán 11 Tập 1 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Bài tập này thường yêu cầu học sinh tính đạo hàm của hàm số, tìm điểm cực trị, hoặc giải các bài toán liên quan đến ứng dụng của đạo hàm.

Nội dung bài tập 5.6 trang 109 SGK Toán 11 Tập 1 - Kết nối tri thức

Bài tập 5.6 thường có dạng như sau:

Cho hàm số f(x) = ... Tìm đạo hàm f'(x).
Tìm các điểm cực trị của hàm số f(x) = ...
Giải phương trình f'(x) = 0.
Khảo sát sự biến thiên của hàm số f(x) = ...

Lời giải chi tiết bài 5.6 trang 109 SGK Toán 11 Tập 1 - Kết nối tri thức

Để giải bài tập này, học sinh cần nắm vững các kiến thức sau:

Các quy tắc tính đạo hàm (quy tắc tính đạo hàm của tổng, hiệu, tích, thương, hàm hợp).
Đạo hàm của các hàm số cơ bản (hàm số đa thức, hàm số lượng giác, hàm số mũ, hàm số logarit).
Điều kiện để hàm số có cực trị.
Cách khảo sát sự biến thiên của hàm số.

Ví dụ, xét bài tập sau:

Cho hàm số f(x) = x³ - 3x² + 2. Tìm đạo hàm f'(x) và tìm các điểm cực trị của hàm số.

Giải:

1. Tính đạo hàm f'(x):

f'(x) = 3x² - 6x

2. Tìm các điểm cực trị:

Để tìm các điểm cực trị, ta giải phương trình f'(x) = 0:

3x² - 6x = 0

3x(x - 2) = 0

Vậy, x = 0 hoặc x = 2

3. Xác định loại cực trị:

Ta xét dấu của f'(x) trên các khoảng:

Khoảng (-∞, 0): f'(x) > 0, hàm số đồng biến.
Khoảng (0, 2): f'(x) < 0, hàm số nghịch biến.
Khoảng (2, +∞): f'(x) > 0, hàm số đồng biến.

Vậy, hàm số có cực đại tại x = 0 và cực tiểu tại x = 2.

Mẹo giải bài tập đạo hàm hiệu quả

Nắm vững các quy tắc tính đạo hàm.
Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
Sử dụng máy tính cầm tay để kiểm tra lại kết quả.
Tham khảo các tài liệu tham khảo, sách giải bài tập để hiểu rõ hơn về kiến thức.

Tại sao nên chọn tusach.vn để học Toán 11?

tusach.vn cung cấp:

Lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 11 Tập 1 - Kết nối tri thức.
Các bài giảng video chất lượng cao, giúp học sinh nắm vững kiến thức.
Các bài tập trắc nghiệm, bài tập tự luyện để học sinh rèn luyện kỹ năng.
Đội ngũ giáo viên giàu kinh nghiệm, sẵn sàng hỗ trợ học sinh khi gặp khó khăn.

Hãy truy cập tusach.vn ngay hôm nay để học Toán 11 hiệu quả!