Bài 4.23 Trang 94 SGK Toán 11 Tập 1 - Kết Nối Tri Thức

Bài 4.23 trang 94 SGK Toán 11 tập 1 - Kết nối tri thức

Bài 4.23 trang 94 SGK Toán 11 Tập 1 - Kết Nối Tri Thức

Bài 4.23 thuộc chương 1: Hàm số và đồ thị của SGK Toán 11 Tập 1 - Kết Nối Tri Thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai, điều kiện xác định và các phép biến đổi hàm số để giải quyết các bài toán cụ thể.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.

Cho hình thang ABCD có hai đáy AB và CD. Qua các điểm A, D lần lượt vẽ các đường thẳng m, n song song với nhau và không nằm trong mặt phẳng (ABCD). Chứng minh rằng mp(B,m) và mp(C,n) song song với nhau.

Đề bài

Cho hình thang ABCD có hai đáy AB và CD. Qua các điểm A, D lần lượt vẽ các đường thẳng m, n song song với nhau và không nằm trong mặt phẳng (ABCD). Chứng minh rằng mp(B,m) và mp(C,n) song song với nhau.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Bài 4.23 trang 94 SGK Toán 11 tập 1 - Kết nối tri thức 1

Nếu mặt phẳng \(\left( \alpha \right)\) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng \(\left( \beta \right)\) thì \(\left( \alpha \right)\) và \(\left( \beta \right)\) song song với nhau.

Lời giải chi tiết

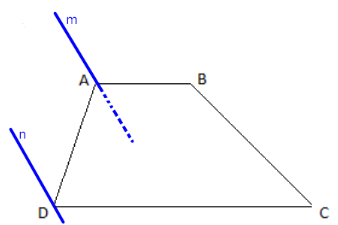
Bài 4.23 trang 94 SGK Toán 11 tập 1 - Kết nối tri thức 2

Ta có: m // n suy ra m // (C,n).

Có: AB // CD (do ABCD là hình thang) suy ra AB // (C,n).

Mặt phẳng (B,m) chứa hai đường thẳng cắt nhau m và AB song song với mp(C,n) suy ra (B,m) // (C,n).

Bài 4.23 Trang 94 SGK Toán 11 Tập 1 - Kết Nối Tri Thức: Giải Chi Tiết và Hướng Dẫn

Bài 4.23 trang 94 SGK Toán 11 Tập 1 - Kết Nối Tri Thức là một bài tập quan trọng trong chương Hàm số và đồ thị. Bài tập này tập trung vào việc xác định tập xác định của hàm số và thực hiện các phép biến đổi hàm số cơ bản. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:

Nội dung bài tập:

Xác định tập xác định của các hàm số sau:

y = √(2x - 1)
y = 1 / (x - 3)
y = √(x + 2) / (x - 1)

Lời giải chi tiết:

Để xác định tập xác định của hàm số, chúng ta cần tìm các giá trị của x sao cho hàm số có nghĩa. Điều này có nghĩa là chúng ta cần đảm bảo rằng các biểu thức trong hàm số không vi phạm bất kỳ điều kiện nào, chẳng hạn như:

Mẫu số khác 0
Biểu thức dưới dấu căn bậc chẵn phải lớn hơn hoặc bằng 0

Giải câu a: y = √(2x - 1)

Hàm số y = √(2x - 1) có nghĩa khi và chỉ khi 2x - 1 ≥ 0. Giải bất phương trình này, ta được:

2x ≥ 1

x ≥ 1/2

Vậy, tập xác định của hàm số là D = [1/2, +∞).

Giải câu b: y = 1 / (x - 3)

Hàm số y = 1 / (x - 3) có nghĩa khi và chỉ khi x - 3 ≠ 0. Giải phương trình này, ta được:

x ≠ 3

Vậy, tập xác định của hàm số là D = R \ {3} (tập hợp tất cả các số thực trừ 3).

Giải câu c: y = √(x + 2) / (x - 1)

Hàm số y = √(x + 2) / (x - 1) có nghĩa khi và chỉ khi cả hai điều kiện sau được thỏa mãn:

x + 2 ≥ 0
x - 1 ≠ 0

Giải các bất phương trình và phương trình này, ta được:

x ≥ -2

x ≠ 1

Vậy, tập xác định của hàm số là D = [-2, 1) ∪ (1, +∞).

Lưu ý quan trọng:

Khi xác định tập xác định của hàm số, hãy luôn kiểm tra kỹ các điều kiện để đảm bảo rằng hàm số có nghĩa với tất cả các giá trị của x trong tập xác định.

Bài tập tương tự:

Để rèn luyện thêm kỹ năng xác định tập xác định của hàm số, bạn có thể làm thêm các bài tập tương tự trong SGK Toán 11 Tập 1 - Kết Nối Tri Thức hoặc các tài liệu tham khảo khác.

Kết luận:

Bài 4.23 trang 94 SGK Toán 11 Tập 1 - Kết Nối Tri Thức là một bài tập cơ bản nhưng quan trọng trong chương Hàm số và đồ thị. Việc nắm vững kiến thức về tập xác định của hàm số sẽ giúp bạn giải quyết các bài toán phức tạp hơn trong tương lai.

Hy vọng lời giải chi tiết và hướng dẫn giải bài tập này sẽ giúp các em học sinh hiểu rõ hơn về bài học và đạt kết quả tốt trong môn Toán.