Giải mục 4 trang 20 SGK Toán 11 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 4 trang 20 SGK Toán 11 tập 1 - Kết nối tri thức
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 11 tập 1 - Kết nối tri thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tốt nhất để giúp bạn nắm vững kiến thức.
Bài giải mục 4 trang 20 tập trung vào các khái niệm quan trọng, giúp bạn hiểu rõ bản chất của vấn đề và áp dụng vào các bài tập khác.
Trong các công thức biến đổi tích thành tổng ở Mục 3, đặt \(u = a - b,\;v = a + b\) và viết các công thức nhận được
Hoạt động 4
Trong các công thức biến đổi tích thành tổng ở Mục 3, đặt \(u = a - b,\;v = a + b\) và viết các công thức nhận được
Lời giải chi tiết:
Ta có: \(u = a - b;v = a + b\).
Suy ra \(u + v = 2a \to a = \frac{{u + v}}{2}\)
\(u - v = 2b \to b = \frac{{u - v}}{2}\)
Ta có: \(\cos u + \cos v = 2\cos \frac{{u + v}}{2}\cos \frac{{u - v}}{2}\)
\(\cos u - \cos v = - 2\sin \frac{{u + v}}{2}\sin \frac{{u - v}}{2}\)
\(\sin u + \sin v = 2\sin \frac{{u + v}}{2}\cos \frac{{u - v}}{2}\)
\(\sin u - \sin v = 2\cos \frac{{u + v}}{2}\sin \frac{{u - v}}{2}\)
Luyện tập 4
Không dùng máy tính, tính giá trị của biểu thức
\(B = \cos \frac{\pi }{9} + \cos \frac{{5\pi }}{9} + \cos \frac{{11\pi }}{9}\).
Phương pháp giải:
Sử dụng công thức: \(\cos u + \cos v = 2\cos \frac{{u + v}}{2}\cos \frac{{u - v}}{2}\)
Lời giải chi tiết:
\(B = \left( {\cos \frac{\pi }{9} + \cos \frac{{5\pi }}{9}} \right) + \cos \frac{{11\pi }}{9} = \left( {2\cos \frac{{\frac{\pi }{9} + \frac{{5\pi }}{9}}}{2}\cos \frac{{\frac{\pi }{9} - \frac{{5\pi }}{9}}}{2}} \right) + \cos \frac{{11\pi }}{9} = 2\cos \frac{\pi }{3}\cos \frac{{2\pi }}{9} + \cos \frac{{11\pi }}{9}\)
\( = \cos \frac{{2\pi }}{9} + \cos \frac{{11\pi }}{9} = 2\cos \frac{{\frac{{2\pi }}{9} + \frac{{11\pi }}{9}}}{2}\cos \frac{{\frac{{2\pi }}{9} - \frac{{11\pi }}{9}}}{2} = 2\cos \frac{{13\pi }}{{18}}\cos \frac{\pi }{2} = 0\)
Vận dụng
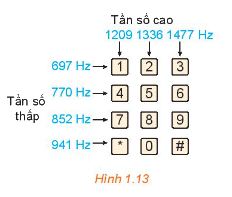
Khi nhấn một phím trên điện thoại cảm ứng, bàn phím sẽ tạo ra hai âm thuần, kết hợp với nhau để tạo ra âm thanh nhận dạng duy nhất phím. Hình 1.13 cho thấy tần số thấp \({f_1}\) và tần số cao \({f_2}\) liên quan đến mỗi phím. Nhấn một phím sẽ tạo ra sóng âm \(y = \sin \left( {2\pi {f_1}t} \right) + \sin \left( {2\pi {f_2}t} \right)\), ở đó t là biến thời gian (tính bằng giây).
a) Tìm hàm số mô hình hóa âm thanh được tạo ra khi nhấn phím 4.
b) Biến đổi công thức vừa tìm được ở câu a về dạng tích của một hàm số sin và một hàm số côsin.
Phương pháp giải:
Sử dụng công thức: \(\sin a + \sin b = 2\sin \frac{{a + b}}{2}\sin \frac{{a - b}}{2}\)
Lời giải chi tiết:
a) Khi nhấn phím 4, ta có sóng âm \(y = \sin \left( {2\pi .770t} \right) + \sin \left( {2\pi .1209t} \right)\)
b) Ta có: \(\sin \left( {2\pi .770t} \right) + \sin \left( {2\pi .1209t} \right) = 2\sin \frac{{2\pi .770t + 2\pi .1209t}}{2}\cos \frac{{2\pi .770t - 2\pi .1209t}}{2}\)
\( = - 2.\sin 1979\pi t.\sin 439\pi t\)
Giải mục 4 trang 20 SGK Toán 11 tập 1 - Kết nối tri thức: Tổng quan và hướng dẫn chi tiết
Mục 4 trang 20 SGK Toán 11 tập 1 - Kết nối tri thức là một phần quan trọng trong chương trình học, tập trung vào việc củng cố kiến thức về hàm số bậc hai và ứng dụng của nó. Để giúp các em học sinh hiểu rõ hơn về nội dung này, tusach.vn xin giới thiệu bài giải chi tiết và dễ hiểu sau đây.
1. Nội dung chính của mục 4 trang 20
Mục 4 trang 20 thường bao gồm các bài tập liên quan đến:
- Xác định các hệ số a, b, c của hàm số bậc hai y = ax2 + bx + c.
- Tìm đỉnh của parabol.
- Xác định trục đối xứng của parabol.
- Vẽ đồ thị hàm số bậc hai.
- Giải các bài toán thực tế liên quan đến hàm số bậc hai.
2. Phương pháp giải các bài tập trong mục 4
Để giải các bài tập trong mục 4 trang 20, các em cần nắm vững các kiến thức sau:
- Công thức tính đỉnh của parabol: xđỉnh = -b/2a, yđỉnh = -Δ/4a (với Δ = b2 - 4ac).
- Phương trình trục đối xứng: x = -b/2a.
- Cách vẽ đồ thị hàm số bậc hai: Xác định đỉnh, trục đối xứng, điểm cắt trục Oy và một vài điểm khác trên đồ thị.
3. Bài giải chi tiết các bài tập trong mục 4
Dưới đây là bài giải chi tiết cho một số bài tập tiêu biểu trong mục 4 trang 20:
Bài 1: Tìm đỉnh của parabol y = 2x2 - 8x + 6
Giải:
Hàm số có dạng y = ax2 + bx + c với a = 2, b = -8, c = 6.
xđỉnh = -b/2a = -(-8)/(2*2) = 2
yđỉnh = -Δ/4a = -((-8)2 - 4*2*6)/(4*2) = - (64 - 48)/8 = -16/8 = -2
Vậy đỉnh của parabol là (2; -2).
Bài 2: Vẽ đồ thị hàm số y = x2 - 4x + 3
Giải:
xđỉnh = -b/2a = -(-4)/(2*1) = 2
yđỉnh = 22 - 4*2 + 3 = -1
Đỉnh của parabol là (2; -1).
Trục đối xứng: x = 2
Điểm cắt trục Oy: (0; 3)
Điểm cắt trục Ox: Giải phương trình x2 - 4x + 3 = 0, ta được x1 = 1, x2 = 3. Vậy các điểm cắt trục Ox là (1; 0) và (3; 0).
Vẽ đồ thị hàm số dựa trên các thông tin trên.
4. Luyện tập thêm
Để củng cố kiến thức và kỹ năng giải bài tập, các em có thể tham khảo thêm các bài tập tương tự trong sách bài tập và các nguồn tài liệu khác. tusach.vn sẽ tiếp tục cập nhật thêm nhiều bài giải chi tiết và hữu ích khác để hỗ trợ các em trong quá trình học tập.
5. Tổng kết
Hy vọng bài giải chi tiết mục 4 trang 20 SGK Toán 11 tập 1 - Kết nối tri thức này sẽ giúp các em hiểu rõ hơn về nội dung bài học và tự tin hơn trong việc giải các bài tập. Chúc các em học tốt!
| Công thức | Mô tả |
|---|---|
| xđỉnh = -b/2a | Hoành độ đỉnh của parabol |
| yđỉnh = -Δ/4a | Tung độ đỉnh của parabol |
| x = -b/2a | Phương trình trục đối xứng |