Giải mục 2 trang 80, 81, 82 SGK Toán 11 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 2 trang 80, 81, 82 SGK Toán 11 tập 1 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 80, 81, 82 SGK Toán 11 tập 1 - Kết nối tri thức. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Bài tập trong mục này tập trung vào các kiến thức về phép biến hình, đặc biệt là phép tịnh tiến và phép quay.
Trong không gian, cho một đường thẳng d và một điểm M không nằm trên d (H.4.21). Gọi (P) là mặt phẳng chứa M và d. a) Trên mặt phẳng (P) có bao nhiêu đường thẳng đi qua M và song song với d? b) Nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) hay không?
HĐ 2
Video hướng dẫn giải
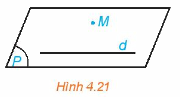
Trong không gian, cho một đường thẳng d và một điểm M không nằm trên d (H.4.21). Gọi (P) là mặt phẳng chứa M và d.
a) Trên mặt phẳng (P) có bao nhiêu đường thẳng đi qua M và song song với d?
b) Nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) hay không?
Phương pháp giải:
Trong không gian, qua một điểm không nằm trên dường thẳng cho trước, có đúng một đường thẳng song song với đường thẳng đã cho
Lời giải chi tiết:
a) Có duy nhất một đường thẳng đi qua M song song với d
b) Nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) vì hai đường thẳng song song đồng phẳng
HĐ 3
Video hướng dẫn giải
Quan sát lớp học và tìm hai đường thẳng song song với mép trên của bảng. Hai đường thẳng đó có song song với nhau hay không?
Phương pháp giải:
Trong không gian, hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau
Lời giải chi tiết:
Đường thẳng song song với mép trên của bảng: Mép dưới của bảng, chân tường bục giảng
Hai đường thẳng đó cũng song song với nhau
LT 3
Video hướng dẫn giải
Trong Ví dụ 1, chứng minh rằng 4 điểm C, D, E, F đồng phẳng và tứ giác CDFE là hình bình hành.
Phương pháp giải:
Để chứng minh bốn điểm: C, D, E, F đồng phẳng ta có thể chứng minh hai đường thẳng AB và CD song song
Dựa vào dấu hiệu tứ giác là hình bình hành để chứng minh CDEF là hình bình hành
Lời giải chi tiết:
Xét hình bình hành ABCD ta có: AB // CD, AB = CD
Xét hình bình hành ABEF ta có: AB // EF, AB = EF
Suy ra EF//CD, EF = CD
Suy ra CDEF là hình bình hành và C, D, E, F đồng phẳng
HĐ 4
Video hướng dẫn giải
Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến c. Một mặt phẳng (R) cắt (P) và (Q) lần lượt theo giao tuyến a và b khác c
a) Nếu hai đường thẳng a và c cắt nhau tại M thì đường thẳng b có đi qua M hay không (H.4.23)? Giải thích vì sao.
b) Nếu hai đường thẳng a và c song song với nhau thì hai đường thẳng b và c có song song với nhau hay không (H.4.24)? Giải thích vì sao.
Phương pháp giải:
Nếu ba mặt phẳng đôi một cắt nhau, theo ba giao tuyến phân biệt thì ba giao tuyến đó đồng quy hoặc đôi một song song với nhau
Lời giải chi tiết:
a) M thuộc c suy ra M nằm trên mp(Q)
M thuộc a suy ra M nằm trên mp(R)
M cùng thuộc mp(R) và (Q) suy ra M nằm trên giao tuyến của mp(R) và (Q)
Như vậy , M thuộc b
LT 4
Video hướng dẫn giải
Trong Ví dụ 4, hãy xác định giao tuyến của hai mặt phẳng (SAD) và (SBC)
Phương pháp giải:
Để xác định giao điểm của một đường thẳng và một mặt phẳng, ta có thể tìm giao điểm của đường thẳng đó với một đường thẳng nằm trong mặt phẳng đã cho.
Lời giải chi tiết:
Hai mp(SAD) và (SBC) có điểm chung S và chứa hai đường thẳng song song AD và BC.
Do đó, giao tuyến của hai mp(SAD) và (SBC) là đường thẳng n đi qua S song cong với AD và BC
VD 2
Video hướng dẫn giải
Một bề kính chứa nước có đáy là hình chữ nhật được đặt nghiêng như Hình 4.26. Giải thích tại sao đường mép nước AB song song với cạnh CD của bề nước

Phương pháp giải:
Nếu hai mặt phẳng chứa hai đường thẳng song song với nhau thì giao tuyến của chúng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó
Lời giải chi tiết:
Ta có: \(mp\left( {ABKI} \right) \cap mp\left( {CDIK} \right) = IK\)
\(mp\left( {ABKI} \right) \cap mp\left( {ABCD} \right) = AB\)
\(mp\left( {CDIK} \right) \cap \left( {ABCD} \right) = CD\)
Mà IK // CD (Do CDIK là hình chữ nhật) suy ra AB // CD.
Giải mục 2 trang 80, 81, 82 SGK Toán 11 tập 1 - Kết nối tri thức: Tổng quan và hướng dẫn chi tiết
Mục 2 của SGK Toán 11 tập 1 - Kết nối tri thức tập trung vào việc củng cố kiến thức về phép biến hình, bao gồm phép tịnh tiến, phép quay và các ứng dụng của chúng trong hình học. Việc nắm vững các khái niệm và kỹ năng giải bài tập trong mục này là vô cùng quan trọng để xây dựng nền tảng vững chắc cho các chương trình học tiếp theo.
Nội dung chính của mục 2
- Phép tịnh tiến: Định nghĩa, tính chất, và cách thực hiện phép tịnh tiến.
- Phép quay: Định nghĩa, tính chất, và cách thực hiện phép quay.
- Ứng dụng của phép biến hình: Giải quyết các bài toán hình học liên quan đến đối xứng, tịnh tiến, và quay.
Giải chi tiết bài tập trang 80
Trang 80 tập trung vào các bài tập vận dụng kiến thức về phép tịnh tiến. Các bài tập thường yêu cầu xác định ảnh của một điểm, một đường thẳng, hoặc một hình qua phép tịnh tiến cho trước. Để giải các bài tập này, các em cần nắm vững công thức tọa độ của ảnh sau phép tịnh tiến: x' = x + a, y' = y + b, trong đó (a, b) là vectơ tịnh tiến.
Giải chi tiết bài tập trang 81
Trang 81 chuyển sang các bài tập về phép quay. Các bài tập này thường yêu cầu xác định ảnh của một điểm, một đường thẳng, hoặc một hình qua phép quay quanh một điểm cho trước với một góc quay nhất định. Công thức tọa độ của ảnh sau phép quay phức tạp hơn phép tịnh tiến và đòi hỏi các em phải hiểu rõ về lượng giác.
Giải chi tiết bài tập trang 82
Trang 82 kết hợp cả phép tịnh tiến và phép quay trong các bài tập. Các bài tập này thường yêu cầu thực hiện liên tiếp hai phép biến hình, hoặc sử dụng phép biến hình để chứng minh một tính chất hình học nào đó. Để giải các bài tập này, các em cần kết hợp kiến thức về cả hai phép biến hình và sử dụng các công thức tọa độ một cách linh hoạt.
Ví dụ minh họa
Bài tập: Cho điểm A(1; 2) và vectơ tịnh tiến v = (3; -1). Tìm tọa độ điểm A' là ảnh của A qua phép tịnh tiến v.
Giải: Sử dụng công thức tọa độ của ảnh sau phép tịnh tiến, ta có:
- x' = 1 + 3 = 4
- y' = 2 + (-1) = 1
Vậy, tọa độ điểm A' là (4; 1).
Lời khuyên khi giải bài tập
- Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
- Vẽ hình minh họa để hình dung rõ hơn về bài toán.
- Sử dụng công thức tọa độ một cách chính xác.
- Kiểm tra lại kết quả sau khi giải xong.
Tusach.vn – Đồng hành cùng bạn học Toán 11
Tusach.vn tự hào là một nguồn tài liệu học tập uy tín và chất lượng, cung cấp đầy đủ lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 11 tập 1 - Kết nối tri thức. Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu hữu ích khác và nâng cao kết quả học tập của bạn!
| Phép biến hình | Công thức tọa độ ảnh |
|---|---|
| Phép tịnh tiến | x' = x + a, y' = y + b |
| Phép quay | x' = x*cos(α) - y*sin(α), y' = x*sin(α) + y*cos(α) |