Giải mục 2 trang 32, 33, 34 SGK Toán 11 tập 1 - Kết nối tri thức

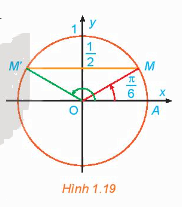
a) Quan sát Hình 1.19, tìm các nghiệm của phương trình đã cho trong nửa khoảng \(\left[ {0;2\pi } \right)\)

b) Dựa vào tính tuần hoàn của hàm số sin, hãy viết công thức nghiệm của phương trình đã cho.

Phương pháp giải:

Nghiệm của phương trình \(\sin x = \frac{1}{2}\) là hoành độ các giao điểm của đường thẳng \(y = \frac{1}{2}\) và đồ thị hàm số \(y = \sin x\)

Lời giải chi tiết:

a) Từ Hình 1.19, ta thấy đường thẳng \(y = \frac{1}{2}\) cắt đường tròn tại 2 điểm M, M’. Ta có nghiệm của phương trình là: \(\frac{\pi }{6}, - \frac{{5\pi }}{6}\)

b) Vì hàm số \(\sin x\) tuần hoàn với chu kỳ là \(2\pi \), ta có công thức nghiệm của phương trình là: \(\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{6} + k2\pi }\\{x = \pi - \frac{\pi }{6} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\)

Giải các phương trình sau: a) \(\sin x = \frac{{\sqrt 2 }}{2}\); b) \(\sin 3x = - \sin 5x\)

Phương pháp giải:

Dựa vào công thức nghiệm tổng quát:

\(\sin x = m\; \Leftrightarrow \sin x = \sin \alpha \;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \alpha + k2\pi }\\{x = \pi - \alpha + k2\pi }\end{array}\left( {k \in \mathbb{Z}} \right)} \right.\)

Áp dụng công thức cộng lượng giác

Lời giải chi tiết:

a) \(\sin x = \frac{{\sqrt 2 }}{2}\;\; \Leftrightarrow \sin x = \sin \frac{\pi }{4}\;\;\;\; \Leftrightarrow \;\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \pi - \frac{\pi }{4} + k2\pi }\end{array}} \right.\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \frac{{3\pi }}{4} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\;\)

b)

\(\begin{array}{l}\sin 3x = - \sin 5x\;\;\;\\\; \Leftrightarrow \,\,\,\sin 3x + \sin 5x = 0\;\;\;\;\;\;\\ \Leftrightarrow \,\,\,2\sin 4x\cos x = 0\;\end{array}\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\sin 4x = 0}\\{\cos x = 0}\end{array}\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\sin 4x = \sin 0}\\{\cos x = \cos \frac{\pi }{2}}\end{array}} \right.\;\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{4x = k\pi }\\{x = \frac{\pi }{2} + k\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.} \right.\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = k\frac{\pi }{4}}\\{x = \frac{\pi }{2} + k\pi }\end{array}(k \in \mathbb{Z})} \right.\)