Giải mục 3 trang 34, 35, 36 SGK Toán 11 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải mục 3 trang 34, 35, 36 SGK Toán 11 tập 2 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết mục 3 trang 34, 35, 36 sách giáo khoa Toán 11 tập 2 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải bài tập trong chương trình học.
tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những tài liệu và lời giải chính xác, dễ hiểu nhất.
Cho đường thẳng a vuông góc với mặt phẳng (P) và song song với đường thẳng b.
HĐ 5
Video hướng dẫn giải
Cho đường thẳng a vuông góc với mặt phẳng (P) và song song với đường thẳng b. Lấy một đường thẳng m bất kì thuộc mặt phẳng (P). Tính (b, m) và từ đó rút ra mối quan hệ giữa b và (P).
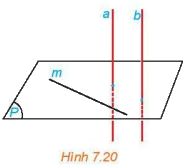
Phương pháp giải:
Cho a, b là 2 đường thẳng phân biệt, nếu đường thẳng b // b’ thì (a, b) = (a, b’)
Lời giải chi tiết:
\(\left. \begin{array}{l}a \bot \left( P \right)\\m \subset \left( P \right)\end{array} \right\} \Rightarrow a \bot m \Rightarrow \left( {a,m} \right) = {90^0}\)
a // b \( \Rightarrow \left( {a,m} \right) = \left( {b,m} \right) = {90^0}\) mà đường thẳng m bất kì thuộc mặt phẳng (P)
\( \Rightarrow \) b \( \bot \) (P).
HĐ 6
Video hướng dẫn giải
Cho hai đường thẳng phân biệt a và b cùng vuông góc với mặt phẳng (P). Xét O là một điểm thuộc a nhưng không thuộc b. Gọi c là đường thẳng qua O và song song với b.

a) Hỏi c có vuông góc với (P) hay không? Nêu nhận xét về vị trí tương đối giữa a và c.
b) Nêu nhận xét về vị trí tương đối giữa hai đường thẳng a và b.
Phương pháp giải:
- Sử dụng kết quả của hoạt động 5 trang 34.
- Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng.
Lời giải chi tiết:
a) b // c; b \( \bot \) (P) \( \Rightarrow \) c \( \bot \) (P)
Mà a \( \bot \) (P)
a, c cùng đi qua điểm O
\( \Rightarrow \) a trùng c.
b) Ta có b // c mà a trùng c nên a // b.
HĐ 7
Video hướng dẫn giải
Cho hai mặt phẳng (P) và (Q) song song với nhau và đường thẳng \(\Delta \) vuông góc với (P). Gọi b là một đường thẳng bất kì thuộc (Q). Lấy một đường thẳng a thuộc (P) sao cho a song song với b (H.7.23). So sánh (\(\Delta \), b) và (\(\Delta \), a). Từ đó rút ra mối quan hệ giữa \(\Delta \) và (Q).

Phương pháp giải:
Sử dụng định nghĩa 2 đường thẳng vuông góc và đường thẳng vuông góc với mặt phẳng.
Lời giải chi tiết:
\(\left. \begin{array}{l}\Delta \bot \left( P \right)\\a \subset \left( P \right)\end{array} \right\} \Rightarrow \Delta \bot a,a//b \Rightarrow \Delta \bot b \Rightarrow \left( {\Delta ,b} \right) = {90^0}\)
\(\Delta \bot a \Rightarrow \left( {\Delta ,a} \right) = {90^0}\)
\( \Rightarrow \) (\(\Delta \), b) = (\(\Delta \), a) mà b là đường thẳng bất kì thuộc (Q)
\( \Rightarrow \) \(\Delta \bot \left( Q \right)\)
HĐ 8
Video hướng dẫn giải
Cho hai mặt phẳng phân biệt (P) và (Q) cùng vuông góc với đường thẳng \(\Delta \). Xét O là một điểm thuộc mặt phẳng (P) nhưng không thuộc mặt phẳng (Q). Gọi (R) là mặt phẳng đi qua O và song song với (Q) (H.7.24).

a) Hỏi (R) có vuông góc với Δ hay không? Nêu nhận xét về vị trí tương đối giữa (P) và (R).
b) Nêu vị trí tương đối giữa (P) và (Q).
Phương pháp giải:
- Sử dụng kết quả của hoạt động 7 trang 35
- Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.
Lời giải chi tiết:
a) (R) // (Q); \(\Delta \) \( \bot \) (Q) \( \Rightarrow \) \(\Delta \) \( \bot \) (R)
Mà \(\Delta \) \( \bot \) (P) và (R), (Q) là 2 mặt phẳng cùng đi qua O
\( \Rightarrow \) (R) trùng (P)
b) (R) // (Q) mà (R) trùng (P) nên (P) // (Q)
LT 3
Video hướng dẫn giải
Một chiếc bàn có các chân cùng vuông góc với mặt phẳng chứa mặt bàn và mặt phẳng chứa mặt sàn. Hỏi hai mặt phẳng đó có song song với nhau hay không? Vì sao?
Phương pháp giải:
Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
Lời giải chi tiết:
Ta coi chân bàn như đường thẳng và mặt bàn, mặt sàn là 2 mặt phẳng.
Một chiếc bàn có các chân cùng vuông góc với mặt phẳng chứa mặt bàn và mặt phẳng chứa mặt sàn nên hai mặt phẳng đó có song song với nhau vì hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
HĐ 9
Video hướng dẫn giải
Cho đường thẳng a song song với mặt phẳng (P) và đường thẳng \(\Delta \) vuông góc với mặt phẳng (P). Tính (\(\Delta \), a).
Phương pháp giải:
Sử dụng định nghĩa 2 đường thẳng vuông góc và đường thẳng vuông góc với mặt phẳng.
Lời giải chi tiết:
Vì a // (P) nên a // b sao cho b \( \subset \) (P)
\( \Rightarrow \) (\(\Delta \); a) = (\(\Delta \); b)
Mà \(\Delta \) \( \bot \) (P); b \( \subset \) (P) nên \(\Delta \) \( \bot \) b \( \Rightarrow \) (\(\Delta \); b) = 900
Vậy (\(\Delta \); a) = 900
HĐ 10
Video hướng dẫn giải
Cho đường thẳng a và mặt phẳng (P) cùng vuông góc với một đường thẳng \(\Delta \).
a) Qua một điểm O thuộc (P), kẻ đường thẳng a' song song với a. Nêu vị trí tương đối giữa a' và (P).
b) Nêu vị trí tương đối giữa a và (P).
Phương pháp giải:
Sử dụng lý thuyết đường thẳng song song với mặt phẳng và đường thẳng vuông góc với mặt phẳng.
Lời giải chi tiết:
a) \(\Delta \bot a,a//a' \Rightarrow \Delta \bot a'\)
\(\Delta \bot a',\Delta \bot \left( P \right)\) \( \Rightarrow \) a' // (P) hoặc a' \( \subset \) (P) mà điểm O thuộc (P) và đi qua a'
Vậy a' \( \subset \) (P).
b) a' // a; a' \( \subset \) (P) \( \Rightarrow \)a // (P) hoặc a \( \subset \) (P) vì a và (P) không phân biệt.
LT 4
Video hướng dẫn giải
Cho hình chóp S.ABCD có đáy ABCD là một hình vuông, SA \( \bot \) (ABCD). Kẻ AH vuông góc với SC (H thuộc SC), BM vuông góc với SC (M thuộc SC). Chứng minh rằng SC \( \bot \) (MBD) và AH // (MBD).

Phương pháp giải:
- Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.
- Trong 1 mặt phẳng có 2 đường thẳng cùng vuông góc với đường thẳng thứ 3 thì chúng song song.
- Đường thẳng song song với mặt phẳng nếu nó song song với 1 đường thẳng nằm trong mặt phẳng đó.
Lời giải chi tiết:
\(\begin{array}{l}\left. \begin{array}{l} + )AC \bot BD\,\,\left( {hv\,\,ABCD} \right)\\SA \bot BD\,\,\left( {SA \bot \left( {ABCD} \right)} \right)\\AC \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BD \bot \left( {SAC} \right)\\\left. \begin{array}{l} + )BD \bot SC\left( {BD \bot \left( {SAC} \right)} \right)\\BM \bot SC\\BD \cap BM = \left\{ B \right\}\end{array} \right\} \Rightarrow SC \bot \left( {MBD} \right)\end{array}\)
Gọi \(AC \cap BD = \left\{ O \right\}\)
\(\left. \begin{array}{l}SC \bot \left( {MBD} \right)\\OM \subset \left( {MBD} \right)\end{array} \right\} \Rightarrow SC \bot OM\)
Mà \(AH \bot SC\)
\( \Rightarrow AH//OM,OM \subset \left( {MBD} \right) \Rightarrow AH//\left( {MBD} \right)\)
Giải mục 3 trang 34, 35, 36 SGK Toán 11 tập 2 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 3 trong SGK Toán 11 tập 2 - Kết nối tri thức thường xoay quanh các chủ đề về đạo hàm của hàm số, bao gồm các quy tắc tính đạo hàm, đạo hàm của các hàm số cơ bản và ứng dụng của đạo hàm trong việc giải các bài toán liên quan đến cực trị, khoảng đơn điệu của hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng để các em học tốt các chương trình Toán học ở các lớp trên.
Nội dung chính của Mục 3
- Đạo hàm của hàm số: Định nghĩa đạo hàm, ý nghĩa hình học và vật lý của đạo hàm.
- Quy tắc tính đạo hàm: Quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số.
- Đạo hàm của các hàm số cơ bản: Đạo hàm của hàm số lũy thừa, hàm số mũ, hàm số logarit, hàm số lượng giác và hàm số ngược của chúng.
- Ứng dụng của đạo hàm: Giải các bài toán tìm cực trị, khoảng đơn điệu của hàm số, và các bài toán liên quan đến tối ưu hóa.
Giải chi tiết các bài tập trang 34, 35, 36
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 3 trang 34, 35, 36 SGK Toán 11 tập 2 - Kết nối tri thức:
Bài 1: (Trang 34)
Đề bài: Tính đạo hàm của các hàm số sau:
- f(x) = x3 + 2x2 - 5x + 1
- g(x) = sin(x) + cos(x)
Lời giải:
- f'(x) = 3x2 + 4x - 5
- g'(x) = cos(x) - sin(x)
Bài 2: (Trang 35)
Đề bài: Tìm đạo hàm của hàm số y = (x2 + 1) / (x - 1)
Lời giải:
Sử dụng quy tắc đạo hàm của thương:
y' = [(x2 + 1)'(x - 1) - (x2 + 1)(x - 1)'] / (x - 1)2
y' = [2x(x - 1) - (x2 + 1)] / (x - 1)2
y' = (x2 - 2x - 1) / (x - 1)2
Bài 3: (Trang 36)
Đề bài: Tìm khoảng đơn điệu của hàm số y = x3 - 3x2 + 2
Lời giải:
y' = 3x2 - 6x
Giải phương trình y' = 0, ta được x = 0 hoặc x = 2
Lập bảng xét dấu y':
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | NB | Giảm | Tăng |
Vậy hàm số đồng biến trên (-∞, 0) và (2, +∞), nghịch biến trên (0, 2).
Lời khuyên khi giải bài tập về đạo hàm
- Nắm vững định nghĩa và ý nghĩa của đạo hàm.
- Thành thạo các quy tắc tính đạo hàm.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính cầm tay để kiểm tra lại kết quả.
Hy vọng với lời giải chi tiết này, các em sẽ hiểu rõ hơn về mục 3 trang 34, 35, 36 SGK Toán 11 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!