Giải mục 3 trang 34, 35 SGK Toán 11 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 3 trang 34, 35 SGK Toán 11 tập 1 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 3 trang 34, 35 sách giáo khoa Toán 11 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em học sinh hiểu rõ các khái niệm và phương pháp giải bài tập liên quan.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và cập nhật nhất để hỗ trợ quá trình học tập của các em.
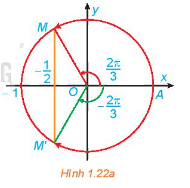
a) Quan sát Hình 1.22a, tìm các nghiệm của phương trình đã cho trong nửa khoảng (left[ { - pi ;pi } right)). b) Dựa vào tính tuần hoản của hàm số cosin, hãy viết công thức nghiệm của phương trình đã cho.
HĐ 3
Video hướng dẫn giải
a) Quan sát Hình 1.22a, tìm các nghiệm của phương trình đã cho trong nửa khoảng \(\left[ { - \pi ;\pi } \right)\).
b) Dựa vào tính tuần hoản của hàm số cosin, hãy viết công thức nghiệm của phương trình đã cho.
Phương pháp giải:
Nghiệm của phương trình \(\cos x = - \frac{1}{2}\) là hoành độ các giao điểm của đường thẳng \(y = - \;\frac{1}{2}\) và đồ thị hàm số \(y = \cos x\)
Lời giải chi tiết:
a) Từ Hình 1.20, ta thấy đường thẳng \(y = \frac{1}{2}\) cắt đường tròn tại 2 điểm M, M’. Ta có nghiệm của phương trình là: \(\frac{\pi }{6}, - \frac{{5\pi }}{6}\)
b) Vì hàm số \(\cos x\) tuần hoàn với chu kỳ là \(2\pi \), ta có công thức nghiệm của phương trình là: \(\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{6} + k2\pi }\\{x = \pi - \frac{\pi }{6} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\)
LT 3
Video hướng dẫn giải
Giải các phương trình sau:
a) \(2\cos x = - \sqrt 2 \); b) \(\cos 3x - \sin 5x = 0\)
Phương pháp giải:
Dựa vào công thức nghiệm tổng quát:
\(\cos x = m\;\; \Leftrightarrow \cos x = \cos \alpha \;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \alpha + k2\pi }\\{x = - \alpha + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\;\)
Lời giải chi tiết:
a) \(2\cos x = - \sqrt 2 \Leftrightarrow \cos x = - \frac{{\sqrt 2 }}{2}\;\; \Leftrightarrow \cos x = \cos \frac{\pi }{4} \Leftrightarrow \;\left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \pi - \frac{\pi }{4} + k2\pi }\end{array}} \right.\;\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{4} + k2\pi }\\{x = \frac{{3\pi }}{4} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\)
b) \(\cos 3x - \sin 5x = 0\;\;\;\; \Leftrightarrow \cos 3x = \sin 5x\;\;\;\; \Leftrightarrow \cos 3x = \cos \left( {\frac{\pi }{2} - 5x} \right)\;\;\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{3x = \frac{\pi }{2} - 5x + k2\pi }\\{3x = - \frac{\pi }{2} + 5x + k2\pi }\end{array}} \right.\;\;\;\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{8x = \frac{\pi }{2} + k2\pi }\\{ - 2x = - \frac{\pi }{2} + k2\pi }\end{array}} \right.\;\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{{16}} + \frac{{k\pi }}{4}}\\{x = \frac{\pi }{4} - k\pi }\end{array}} \right.\;\;\left( {k \in \mathbb{Z}} \right)\)
VD
Video hướng dẫn giải
Khi mặt trăng quay quanh Trái Đất, mặt đối diện với Trái Đất thường chỉ được Mặt Trời chiếu sáng một phần. Các pha của Mặt Trăng mô tả mức độ phần bề mặt của nó được Mặt Trời chiếu sáng. Khi góc giữa Mặt Trời, Trái Đất và Mặt Trăng là \(\alpha \left( {{0^0} \le \;\alpha \le {{360}^0}} \right)\)thì tỉ lệ F của phần Mặt Trăng được chiếu sáng cho bới công thức:
\(F = \frac{1}{2}\left( {1 - \cos \alpha } \right)\).

Xác định góc \(\alpha \) tương ứng với các pha sau của Mặt Trăng.
a) \(F = 0\) (trăng mới)
b) \(F = 0,25\) (trăng lưỡi liềm)
c) \(F = 0,5\) (trăng bán nguyệt đầu tháng hoặc trăng bán nguyệt cuối tháng)
d) \(F = 1\) (trăng tròn)
Phương pháp giải:
Thay giá trị F tương ứng rồi giải phương trình để tìm \(\alpha \)
Lời giải chi tiết:
a)
\(\begin{array}{l}F = 0\;\\ \Rightarrow \frac{1}{2}\left( {1 - \cos \alpha } \right) = 0\;\; \Leftrightarrow 1 - \cos \alpha = 0\;\; \Leftrightarrow \cos \alpha = 1\; \Leftrightarrow \alpha = k2\pi \;\left( {k \in \mathbb{Z}} \right)\end{array}\)
b) \(F = 0,25\; \Rightarrow \frac{1}{2}\left( {1 - \cos \alpha } \right) = 0,25\; \Leftrightarrow 1 - \cos \alpha = \frac{1}{2}\;\; \Leftrightarrow \cos \alpha = \frac{1}{2}\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\alpha = \frac{\pi }{3} + k2\pi }\\{\alpha = - \frac{\pi }{3} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\)
c) \(F = 0,5\;\; \Rightarrow \frac{1}{2}\left( {1 - \cos \alpha } \right) = 0,5\; \Leftrightarrow 1 - \cos \alpha = 1\; \Leftrightarrow \cos \alpha = 0\; \Leftrightarrow \alpha = \frac{\pi }{2} + k\pi \;\;\left( {k \in \mathbb{Z}} \right)\)
d) \(F = 1\; \Leftrightarrow \frac{1}{2}\left( {1 - \cos \alpha } \right) = 1\;\; \Leftrightarrow 1 - \cos \alpha = 2\; \Leftrightarrow \cos \alpha = - 1\; \Leftrightarrow \alpha = \pi + k2\pi \;\left( {k \in \mathbb{Z}} \right)\)
Giải mục 3 trang 34, 35 SGK Toán 11 tập 1 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 3 trang 34, 35 SGK Toán 11 tập 1 - Kết nối tri thức tập trung vào việc ôn tập chương 1: Hàm số và đồ thị. Đây là một phần quan trọng trong chương trình Toán 11, đặt nền móng cho các kiến thức tiếp theo. Việc nắm vững các khái niệm và kỹ năng giải bài tập trong mục này là vô cùng cần thiết.
Nội dung chính của Mục 3
- Ôn tập về hàm số: Các loại hàm số (hàm số bậc nhất, hàm số bậc hai, hàm số mũ, hàm số logarit), tập xác định, tập giá trị, tính đơn điệu, cực trị.
- Đồ thị hàm số: Cách vẽ đồ thị hàm số, các điểm đặc biệt trên đồ thị (điểm cực trị, điểm uốn, giao điểm với các trục tọa độ).
- Ứng dụng của hàm số: Giải các bài toán thực tế liên quan đến hàm số.
Các dạng bài tập thường gặp
- Xác định tập xác định của hàm số: Yêu cầu học sinh phải nắm vững điều kiện xác định của các loại hàm số khác nhau.
- Tìm tập giá trị của hàm số: Sử dụng các phương pháp như xét hàm số trên một khoảng, sử dụng đạo hàm để tìm cực trị.
- Khảo sát sự biến thiên của hàm số: Tìm đạo hàm, xét dấu đạo hàm để xác định khoảng đồng biến, nghịch biến, cực trị.
- Vẽ đồ thị hàm số: Xác định các điểm đặc biệt, vẽ đồ thị dựa trên các thông tin đã tìm được.
- Giải phương trình, bất phương trình: Sử dụng các kiến thức về hàm số để giải quyết các bài toán phương trình, bất phương trình.
Hướng dẫn giải chi tiết các bài tập trong SGK
Dưới đây là hướng dẫn giải chi tiết các bài tập trong mục 3 trang 34, 35 SGK Toán 11 tập 1 - Kết nối tri thức:
Bài 1: (Trang 34)
Đề bài: (Ví dụ: Xác định tập xác định của hàm số y = √(x-2)/(x+1))
Lời giải: Để hàm số y = √(x-2)/(x+1) xác định, cần có x-2 ≥ 0 và x+1 ≠ 0. Từ đó suy ra x ≥ 2 và x ≠ -1. Vậy tập xác định của hàm số là [2, +∞).
Bài 2: (Trang 35)
Đề bài: (Ví dụ: Tìm khoảng đồng biến, nghịch biến của hàm số y = x2 - 4x + 3)
Lời giải: Tính đạo hàm y' = 2x - 4. Xét dấu y': y' > 0 khi x > 2, hàm số đồng biến trên (2, +∞). y' < 0 khi x < 2, hàm số nghịch biến trên (-∞, 2).
Mẹo học tập hiệu quả
- Nắm vững định nghĩa và tính chất của các loại hàm số.
- Luyện tập thường xuyên các bài tập khác nhau.
- Sử dụng đồ thị hàm số để hiểu rõ hơn về sự biến thiên của hàm số.
- Kết hợp kiến thức về hàm số với các kiến thức khác trong chương trình Toán 11.
Tài liệu tham khảo thêm
Ngoài SGK, các em có thể tham khảo thêm các tài liệu sau:
- Sách bài tập Toán 11
- Các trang web học Toán trực tuyến
- Các video bài giảng Toán 11
Tusach.vn hy vọng bài viết này sẽ giúp các em học sinh giải quyết tốt các bài tập trong mục 3 trang 34, 35 SGK Toán 11 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!