Bài 4.24 Trang 94 SGK Toán 11 Tập 1 - Kết Nối Tri Thức

Bài 4.24 trang 94 SGK Toán 11 tập 1 - Kết nối tri thức

Bài 4.24 trang 94 SGK Toán 11 Tập 1 - Kết Nối Tri Thức

Bài 4.24 thuộc chương 1: Hàm số và đồ thị của SGK Toán 11 Tập 1 - Kết Nối Tri Thức. Bài tập này yêu cầu học sinh vận dụng kiến thức về hàm số bậc hai, điều kiện xác định và tính đơn điệu của hàm số để giải quyết các bài toán cụ thể.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.

Cho hình tứ diện SABC. Trên cạnh SA lấy các điểm ({A_1},{A_2})sao cho (A{A_1} = {A_1}{A_2} = {A_2}S.) Gọi (P) và (Q) là hai mặt phẳng song song với mặt phẳng (ABC) và lần lượt đi qua ({A_1},{A_2}.) Mặt phẳng (P) cắt các cạnh SB, SC lần lượt tại ({B_1},{C_1}.) Mặt phẳng (Q) cắt các canhj SB, SC lần lượt tại ({B_2},{C_2}.) Chứng minh (B{B_1} = {B_1}{B_2} = {B_2}S) và (C{C_1} = {C_1}{C_2} = {C_2}S).

Đề bài

Cho hình tứ diện SABC. Trên cạnh SA lấy các điểm \({A_1},{A_2}\)sao cho \(A{A_1} = {A_1}{A_2} = {A_2}S.\) Gọi (P) và (Q) là hai mặt phẳng song song với mặt phẳng (ABC) và lần lượt đi qua \({A_1},{A_2}.\) Mặt phẳng (P) cắt các cạnh SB, SC lần lượt tại \({B_1},{C_1}.\) Mặt phẳng (Q) cắt các canhj SB, SC lần lượt tại \({B_2},{C_2}.\) Chứng minh \(B{B_1} = {B_1}{B_2} = {B_2}S\) và \(C{C_1} = {C_1}{C_2} = {C_2}S\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Bài 4.24 trang 94 SGK Toán 11 tập 1 - Kết nối tri thức 1

Ba mặt phẳng đôi một song song chắn trên hai cát tuyến phân biệt bất kì những đoạn thẳng tương ứng tỉ lệ.

Lời giải chi tiết

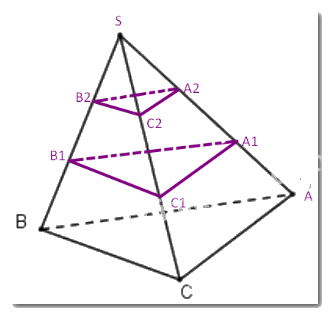
Bài 4.24 trang 94 SGK Toán 11 tập 1 - Kết nối tri thức 2

Áp dụng định lí Thales cho ba mặt phẳng (ABC), (P), (Q) và hai cát tuyến SA, SC ta có:

\(\frac{{{C_2}S}}{{{A_2}S}} = \frac{{{C_1}{C_2}}}{{{A_1}{A_{2\;}}}} = \frac{{C{C_1}}}{{A{A_1}}}\) mà \(A{A_1} = {A_1}{A_2} = {A_2}S\).

Suy ra \(C{C_1} = {C_1}{C_2} = {C_2}S\). Áp dụng định lí Thales cho ba mặt phẳng (ABC), (P), (Q) và hai cát tuyến SA, SB ta có:

\(\frac{{{B_2}S}}{{{A_2}S}} = \frac{{{B_1}{B_2}}}{{{A_1}{A_2}}} = \frac{{B{B_1}}}{{A{A_1}}}\) mà \(A{A_1} = A{A_2} = {A_2}S\).

Suy ra \(B{B_1} = {B_1}{B_2} = {B_2}S\).

Bài 4.24 Trang 94 SGK Toán 11 Tập 1 - Kết Nối Tri Thức: Giải Chi Tiết và Hướng Dẫn

Bài 4.24 trang 94 SGK Toán 11 Tập 1 - Kết Nối Tri Thức là một bài tập quan trọng trong chương Hàm số và đồ thị. Bài tập này thường yêu cầu học sinh phân tích hàm số bậc hai, xác định tập xác định, tìm khoảng đồng biến, nghịch biến và vẽ đồ thị hàm số. Dưới đây là giải chi tiết bài 4.24, cùng với hướng dẫn từng bước để bạn có thể tự giải và hiểu rõ hơn về kiến thức này.

Nội dung bài tập 4.24

Thông thường, bài 4.24 sẽ đưa ra một hàm số bậc hai có dạng y = ax² + bx + c và yêu cầu:

Xác định tập xác định của hàm số.
Tìm tọa độ đỉnh của parabol.
Tìm trục đối xứng của parabol.
Xác định khoảng đồng biến, nghịch biến của hàm số.
Vẽ đồ thị hàm số.

Giải chi tiết bài 4.24 (Ví dụ minh họa)

Giả sử hàm số được cho là: y = x² - 4x + 3

Bước 1: Xác định tập xác định

Hàm số bậc hai có tập xác định là R (tập hợp tất cả các số thực).

Bước 2: Tìm tọa độ đỉnh của parabol

Tọa độ đỉnh của parabol có dạng I(x₀, y₀), với:

x₀ = -b / 2a
y₀ = f(x₀)

Trong trường hợp này, a = 1, b = -4, c = 3. Vậy:

x₀ = -(-4) / (2 * 1) = 2
y₀ = (2)² - 4 * 2 + 3 = -1

Vậy tọa độ đỉnh của parabol là I(2, -1).

Bước 3: Tìm trục đối xứng của parabol

Trục đối xứng của parabol là đường thẳng x = x₀, tức là x = 2.

Bước 4: Xác định khoảng đồng biến, nghịch biến

Vì a = 1 > 0, parabol có dạng mở lên trên. Do đó:

Hàm số nghịch biến trên khoảng (-∞, 2)
Hàm số đồng biến trên khoảng (2, +∞)

Bước 5: Vẽ đồ thị hàm số

Để vẽ đồ thị hàm số, ta cần xác định một vài điểm thuộc đồ thị, ví dụ:

x	y
0	3
1	0
3	0
4	3

Vẽ parabol đi qua các điểm này, có đỉnh I(2, -1) và trục đối xứng x = 2.

Lưu ý khi giải bài tập 4.24

Luôn xác định đúng hệ số a, b, c của hàm số bậc hai.
Sử dụng công thức tính tọa độ đỉnh và trục đối xứng một cách chính xác.
Chú ý đến dấu của hệ số a để xác định chiều mở của parabol và khoảng đồng biến, nghịch biến.
Vẽ đồ thị hàm số một cách cẩn thận, đảm bảo các điểm thuộc đồ thị được xác định chính xác.

Hy vọng với hướng dẫn chi tiết này, bạn có thể tự tin giải quyết bài 4.24 trang 94 SGK Toán 11 Tập 1 - Kết Nối Tri Thức một cách hiệu quả. Hãy luyện tập thêm nhiều bài tập tương tự để nắm vững kiến thức và kỹ năng giải toán nhé!