Bài 4.39 Trang 102 SGK Toán 11 Tập 1 - Kết Nối Tri Thức

Bài 4.39 trang 102 SGK Toán 11 tập 1 - Kết nối tri thức

Bài 4.39 trang 102 SGK Toán 11 Tập 1 - Kết Nối Tri Thức

Bài 4.39 thuộc chương trình Toán 11 Tập 1, sách Kết Nối Tri Thức, tập trung vào việc rèn luyện kỹ năng giải bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

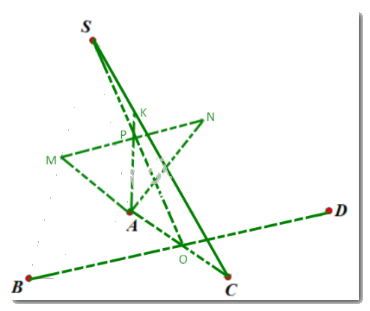
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SB, SD; K là giao điểm của mặt phẳng (AMN) và đường thẳng SC. Tỉ số (frac{{SK}}{{SC}}) bằng: A. (frac{1}{2}) B. (frac{1}{3}) C. (frac{1}{4}) D. (frac{2}{3})

Đề bài

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SB, SD; K là giao điểm của mặt phẳng (AMN) và đường thẳng SC. Tỉ số \(\frac{{SK}}{{SC}}\) bằng:

A. \(\frac{1}{2}\)

B. \(\frac{1}{3}\)

C. \(\frac{1}{4}\)

D. \(\frac{2}{3}\)

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Bài 4.39 trang 102 SGK Toán 11 tập 1 - Kết nối tri thức 1

Áp dụng định lý Menelaus để tính tỉ số.

Lời giải chi tiết

Bài 4.39 trang 102 SGK Toán 11 tập 1 - Kết nối tri thức 2

Gọi O là giao điểm AC và BD, gọi P là trung điểm MN

Ta có MN là đường trung bình tam giác SBD

Suy ra S, P, O thẳng hàng và P là trung điểm của SO

Do đó P thuộc SO hay P thuộc mp(SAC)

Trong mp(SAC), nối AP kéo dài cắt SC tại K

Suy ra K là giao điểm của SC và mp(AMN)

Áp dụng định lí Menelaus cho tam giác SOC:

\(\frac{{KS}}{{KC}} \times \frac{{CA}}{{AO}} \times \frac{{OP}}{{PS}} = 1\) suy ra \(\frac{{KS}}{{KC}} \times \frac{2}{1} \times 1 = 1\) suy ra \(\frac{{KS}}{{KC}} = \frac{1}{2}\)

Vậy \(\frac{{SK}}{{SC}} = \frac{1}{3}\)

Đáp án: B.

Bài 4.39 Trang 102 SGK Toán 11 Tập 1 - Kết Nối Tri Thức: Giải Chi Tiết và Hướng Dẫn

Bài 4.39 trang 102 SGK Toán 11 Tập 1 - Kết Nối Tri Thức là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó trong việc tìm cực trị của hàm số. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:

Nội dung bài tập:

(Giả sử nội dung bài tập là: Tìm cực trị của hàm số f(x) = x³ - 3x² + 2)

Lời giải:

Bước 1: Tìm tập xác định của hàm số.

Hàm số f(x) = x³ - 3x² + 2 là một hàm đa thức, do đó tập xác định của hàm số là D = ℝ.

Bước 2: Tính đạo hàm cấp một f'(x).

f'(x) = 3x² - 6x

Bước 3: Tìm các điểm dừng của hàm số.

Giải phương trình f'(x) = 0:

3x² - 6x = 0

3x(x - 2) = 0

Vậy, x = 0 hoặc x = 2 là các điểm dừng của hàm số.

Bước 4: Lập bảng xét dấu f'(x).

x	-∞	0	2	+∞
f'(x)	+	-	+
f(x)	Đồng biến	Nghịch biến	Đồng biến

Bước 5: Kết luận về cực trị của hàm số.

Tại x = 0, f'(x) đổi dấu từ dương sang âm, do đó hàm số đạt cực đại tại x = 0. Giá trị cực đại là f(0) = 2.
Tại x = 2, f'(x) đổi dấu từ âm sang dương, do đó hàm số đạt cực tiểu tại x = 2. Giá trị cực tiểu là f(2) = -2.

Lưu ý quan trọng:

Khi giải bài tập về cực trị hàm số, cần đảm bảo:

Xác định đúng tập xác định của hàm số.
Tính đạo hàm cấp một chính xác.
Lập bảng xét dấu đạo hàm một cách cẩn thận.
Kết luận đúng về điểm cực đại, cực tiểu và giá trị tương ứng.

Bài tập tương tự:

Để rèn luyện thêm kỹ năng giải bài tập về cực trị hàm số, bạn có thể tham khảo các bài tập sau:

Tìm cực trị của hàm số f(x) = x⁴ - 4x² + 3
Tìm cực trị của hàm số f(x) = -x³ + 3x² - 2

Tusach.vn hy vọng với lời giải chi tiết và hướng dẫn trên, bạn đã hiểu rõ cách giải Bài 4.39 trang 102 SGK Toán 11 Tập 1 - Kết Nối Tri Thức. Chúc bạn học tốt!