Bài 4.2 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức
Tổng quan nội dung
Bài 4.2 trang 77 SGK Toán 11 Tập 1 - Kết Nối Tri Thức
Bài 4.2 trang 77 SGK Toán 11 Tập 1 thuộc chương trình học Toán 11 Kết Nối Tri Thức, tập trung vào việc luyện tập về đạo hàm của hàm số. Bài tập này yêu cầu học sinh vận dụng các kiến thức đã học để tính đạo hàm của các hàm số phức tạp hơn.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập một cách hiệu quả.
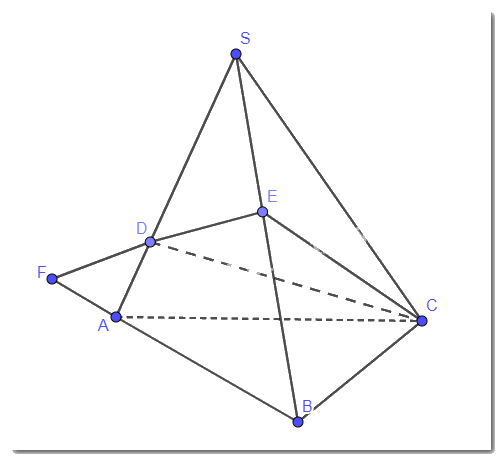
Cho tam giác ABC và điểm S không thuộc mặt phẳng (ABC). Lấy D, E là các điểm lần lượt thuộc các cạnh SA, SB và D, E khác S. a) Đường thẳng DE có nằm trong mặt phẳng (SAB) không? b) Giả sử DE cắt AB tại F. Chứng minh rằng F là điểm chung của hai mặt phẳng (SAB) và (CDE).
Đề bài
Cho tam giác ABC và điểm S không thuộc mặt phẳng (ABC). Lấy D, E là các điểm lần lượt thuộc các cạnh SA, SB và D, E khác S.
a) Đường thẳng DE có nằm trong mặt phẳng (SAB) không?
b) Giả sử DE cắt AB tại F. Chứng minh rằng F là điểm chung của hai mặt phẳng (SAB) và (CDE).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì tất cả các điểm của đường thẳng đều thuộc mặt phẳng đó.
Để xác định giao điểm của một đường thẳng và một mặt phẳng, ta có thể tìm giao điểm của đường thẳng đó với một đường thẳng nằm trong mặt phẳng đã cho.
Lời giải chi tiết
a) Ta có các điểm D, E đều nằm trong mp(SAB) nên đường thẳng DE nằm trong mp (SAB).
b) F thuộc AB suy ra F nằm trong mp (SAB).
F thuộc DE suy ra F nằm trong mp(CDE).
Do đó, F là điểm chung của hai mặt phẳng (SAB)và (CDE).
Giải Bài 4.2 Trang 77 SGK Toán 11 Tập 1 - Kết Nối Tri Thức Chi Tiết
Bài 4.2 trang 77 SGK Toán 11 Tập 1 - Kết Nối Tri Thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Để giải bài tập này, chúng ta cần nắm vững các quy tắc tính đạo hàm cơ bản, bao gồm đạo hàm của tổng, hiệu, tích, thương và đạo hàm của hàm hợp.
Nội dung bài tập 4.2 trang 77 SGK Toán 11 Tập 1 - Kết Nối Tri Thức
Bài tập yêu cầu tính đạo hàm của các hàm số sau:
- f(x) = x3 - 3x2 + 2x - 5
- g(x) = (x2 + 1)(x - 2)
- h(x) = 1/x2
- k(x) = sin(2x)
Hướng dẫn giải chi tiết
1. Giải f(x) = x3 - 3x2 + 2x - 5
Áp dụng quy tắc đạo hàm của tổng và hiệu, ta có:
f'(x) = (x3)' - (3x2)' + (2x)' - (5)'
f'(x) = 3x2 - 6x + 2 - 0
f'(x) = 3x2 - 6x + 2
2. Giải g(x) = (x2 + 1)(x - 2)
Áp dụng quy tắc đạo hàm của tích, ta có:
g'(x) = (x2 + 1)'(x - 2) + (x2 + 1)(x - 2)'
g'(x) = (2x)(x - 2) + (x2 + 1)(1)
g'(x) = 2x2 - 4x + x2 + 1
g'(x) = 3x2 - 4x + 1
3. Giải h(x) = 1/x2
Viết lại hàm số h(x) = x-2. Áp dụng quy tắc đạo hàm của lũy thừa, ta có:
h'(x) = -2x-3
h'(x) = -2/x3
4. Giải k(x) = sin(2x)
Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
k'(x) = cos(2x) * (2x)'
k'(x) = cos(2x) * 2
k'(x) = 2cos(2x)
Lưu ý khi giải bài tập về đạo hàm
- Nắm vững các quy tắc đạo hàm cơ bản.
- Biết cách áp dụng quy tắc đạo hàm của hàm hợp.
- Kiểm tra lại kết quả sau khi tính đạo hàm.
- Luyện tập thường xuyên để nâng cao kỹ năng giải bài tập.
Bài tập tương tự
Để củng cố kiến thức, bạn có thể luyện tập thêm các bài tập tương tự sau:
- Tính đạo hàm của hàm số y = x4 + 2x3 - x + 1
- Tính đạo hàm của hàm số y = (x2 - 3x + 2)(x + 1)
- Tính đạo hàm của hàm số y = 1/(x + 2)
- Tính đạo hàm của hàm số y = cos(3x)
tusach.vn hy vọng với lời giải chi tiết và hướng dẫn trên, bạn đã hiểu rõ cách giải Bài 4.2 trang 77 SGK Toán 11 Tập 1 - Kết Nối Tri Thức. Chúc bạn học tốt!