Giải mục 4 trang 26, 27 SGK Toán 11 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 4 trang 26, 27 SGK Toán 11 tập 1 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết mục 4 trang 26, 27 sách giáo khoa Toán 11 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ cung cấp đáp án và hướng dẫn giải các bài tập trong mục, giúp các em hiểu rõ kiến thức và rèn luyện kỹ năng giải toán.
tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Cho hàm số (y = cos x) a) Xét tính chẵn, lẻ của hàm số
HĐ 5
Cho hàm số \(y = \cos x\)
a) Xét tính chẵn, lẻ của hàm số
b) Hoàn thành bảng giá trị của hàm số \(y = \cos x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) bằng cách tính giá trị của \(\cos x\) với những x không âm, sau đó sử dụng kết quả câu a để suy ra giá trị tương ứng của \(\cos x\) với những x âm.
\(x\) | \( - \pi \) | \( - \frac{{3\pi }}{4}\) | \( - \frac{\pi }{2}\) | \( - \frac{\pi }{4}\) | 0 | \(\frac{\pi }{4}\) | \(\frac{\pi }{2}\) | \(\frac{{3\pi }}{4}\) | \(\pi \) |
\(\cos x\) | ? | ? | ? | ? | ? | ? | ? | ? | ? |
Bằng cách lấy nhiều điểm \(M\left( {x;\sin x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \cos x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\).
c) Bằng cách làm tương tự câu b cho các đoạn khác có độ dài bằng chu kỳ \(T = 2\pi \), ta được đồ thị của hàm số \(y = \cos x\) như hình dưới đây.
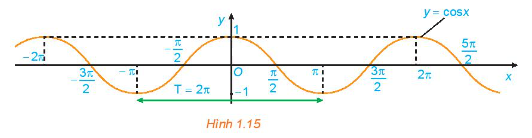
Từ đồ thị ở Hình 1.15, hãy cho biết tập giá trị, các khoảng đồng biến, các khoảng nghịch biến của hàm số \(y = \cos x\)
Phương pháp giải:
Sử dụng định nghĩa hàm số chẵn lẻ
Dựa vào đồ thị để xác định tập giá trị, các khoảng đồng biến, nghịch biến của hàm số
Lời giải chi tiết:
a) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \cos \left( { - x} \right) = \cos x = f\left( x \right),\;\forall x\; \in \;D\)
Vậy \(y = \cos x\) là hàm số chẵn.
b)
\(x\) | \( - \pi \) | \( - \frac{{3\pi }}{4}\) | \( - \frac{\pi }{2}\) | \( - \frac{\pi }{4}\) | 0 | \(\frac{\pi }{4}\) | \(\frac{\pi }{2}\) | \(\frac{{3\pi }}{4}\) | \(\pi \) |
\(\cos x\) | \( - 1\) | \( - \frac{{\sqrt 2 }}{2}\) | \(0\) | \(\frac{{\sqrt 2 }}{2}\) | 1 | \(\frac{{\sqrt 2 }}{2}\) | 0 | \( - \frac{{\sqrt 2 }}{2}\) | \( - 1\) |
c) Từ đồ thị trên, ta thấy hàm số \(y = \cos x\) có tập xác định là \(\mathbb{R}\), tập giá trị là [-1;1] và đồng biến trên mỗi khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi + k2\pi } \right),\;k\; \in \;\mathbb{Z}\)
LT
Tìm tập giá trị của hàm số \(y = - 3\cos x.\)
Phương pháp giải:
Tập giá trị của hàm số là tập min – max của hàm số trên tập xác định
Lời giải chi tiết:
Tập xác định của hàm số là \(D = \mathbb{R}\)
Vì
\( \Rightarrow \) Tập giá trị của hàm số \(y = - 3\cos x\) là \(T = \left[ { - 3;3} \right]\).
VD
Trong vật lí, ta biết rằng phương trình tổng quát của một vật dao động điều hòa cho bởi công thức \(x\left( t \right) = A\cos (\omega t + \varphi )\), trong đó t là thời điểm (tính bằng giây), x(t) là li độ của vật tại thời điểm t, A là biên độ dao động (A > 0), \(\omega t + \varphi \) là pha dao động tại thời điểm t và \(\varphi \in \left[ { - \pi ;\pi } \right]\) là pha ban đầu của dao động. Dao động điều hòa này có chu kỳ \(T = \frac{{2\pi }}{\omega }\) (tức là khoảng thời gian để vật thực hiện một dao động toàn phần).
Giả sử một vật dao động điều hòa theo phương trình \(x\left( t \right) = - 5\cos 4\pi t\) (cm).
a) Hãy xác định biên độ và pha ban đầu của dao động.
b) Tính pha của dao động tại thời điểm \(t = 2\) (giây). Hỏi trong khoảng thời gian 2 giây, vật thực hiện được bao nhiêu dao động toàn phần?
Phương pháp giải:
Dựa vào phương trình tổng quát để xác định: Biên độ dao động, Pha dao động tại thời điểm t, Pha ban đầu
Lời giải chi tiết:
a) Ta có: – 5cos 4πt = 5cos(4πt + π).
Biên độ dao động \(A = 5 > 0\); Pha ban đầu của dao động: \(\varphi = \pi\)
b) Pha dao động tại thời điểm \(t = 2\) là \(\omega t + \varphi = 4\pi .2 + \pi = 9\pi \)
Chu kỳ \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{4\pi }} = 0,5\)
Trong khoảng thời gian 2 giây, số dao động toàn phần vật thực hiện được là: \(\frac{2}{{0,5}} = 4\) (dao động)
Giải mục 4 trang 26, 27 SGK Toán 11 tập 1 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 4 trang 26, 27 SGK Toán 11 tập 1 - Kết nối tri thức tập trung vào việc ôn tập chương 1: Hàm số và đồ thị. Nội dung chính bao gồm các dạng bài tập về xác định tập xác định của hàm số, tìm tập giá trị, xét tính chẵn lẻ của hàm số, và vẽ đồ thị hàm số. Việc nắm vững kiến thức nền tảng về hàm số là vô cùng quan trọng để giải quyết các bài toán trong chương trình Toán 11.
Nội dung chi tiết các bài tập trong mục 4
Bài 1: Xác định tập xác định của hàm số
Bài tập này yêu cầu học sinh xác định tập xác định của các hàm số được cho. Để giải bài tập này, cần nhớ các điều kiện để hàm số có nghĩa, ví dụ như mẫu số khác 0, biểu thức dưới dấu căn lớn hơn hoặc bằng 0, và logarit có cơ số lớn hơn 0 và khác 1.
- Ví dụ: Hàm số y = √(x - 2) có tập xác định là [2, +∞)
- Lưu ý: Cần kiểm tra kỹ các điều kiện để đảm bảo tính chính xác của kết quả.
Bài 2: Tìm tập giá trị của hàm số
Bài tập này yêu cầu học sinh tìm tập giá trị của các hàm số được cho. Để giải bài tập này, có thể sử dụng phương pháp xét hàm số hoặc sử dụng các tính chất của hàm số.
- Bước 1: Xác định tập xác định của hàm số.
- Bước 2: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên tập xác định.
- Bước 3: Kết luận tập giá trị của hàm số.
Bài 3: Xét tính chẵn lẻ của hàm số
Bài tập này yêu cầu học sinh xét tính chẵn lẻ của các hàm số được cho. Để giải bài tập này, cần kiểm tra xem hàm số có thỏa mãn điều kiện f(-x) = f(x) (hàm chẵn) hoặc f(-x) = -f(x) (hàm lẻ) hay không.
Ví dụ: Hàm số y = x2 là hàm chẵn vì y(-x) = (-x)2 = x2 = y(x).
Bài 4: Vẽ đồ thị hàm số
Bài tập này yêu cầu học sinh vẽ đồ thị của các hàm số được cho. Để vẽ đồ thị hàm số, cần xác định các điểm đặc biệt của đồ thị, ví dụ như giao điểm với các trục tọa độ, điểm cực trị, và tiệm cận.
Phương pháp giải bài tập hiệu quả
Để giải các bài tập trong mục 4 trang 26, 27 SGK Toán 11 tập 1 - Kết nối tri thức một cách hiệu quả, cần:
- Nắm vững kiến thức cơ bản về hàm số.
- Luyện tập thường xuyên các dạng bài tập khác nhau.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi và phần mềm vẽ đồ thị.
- Kiểm tra lại kết quả sau khi giải bài tập.
Bảng tổng hợp các công thức quan trọng
| Công thức | Mô tả |
|---|---|
| Tập xác định | Tập hợp các giá trị của x sao cho hàm số có nghĩa. |
| Tập giá trị | Tập hợp các giá trị của y mà hàm số có thể đạt được. |
| Hàm chẵn | f(-x) = f(x) |
| Hàm lẻ | f(-x) = -f(x) |
Kết luận
Hy vọng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 4 trang 26, 27 SGK Toán 11 tập 1 - Kết nối tri thức. Chúc các em học tập tốt và đạt kết quả cao trong môn Toán!