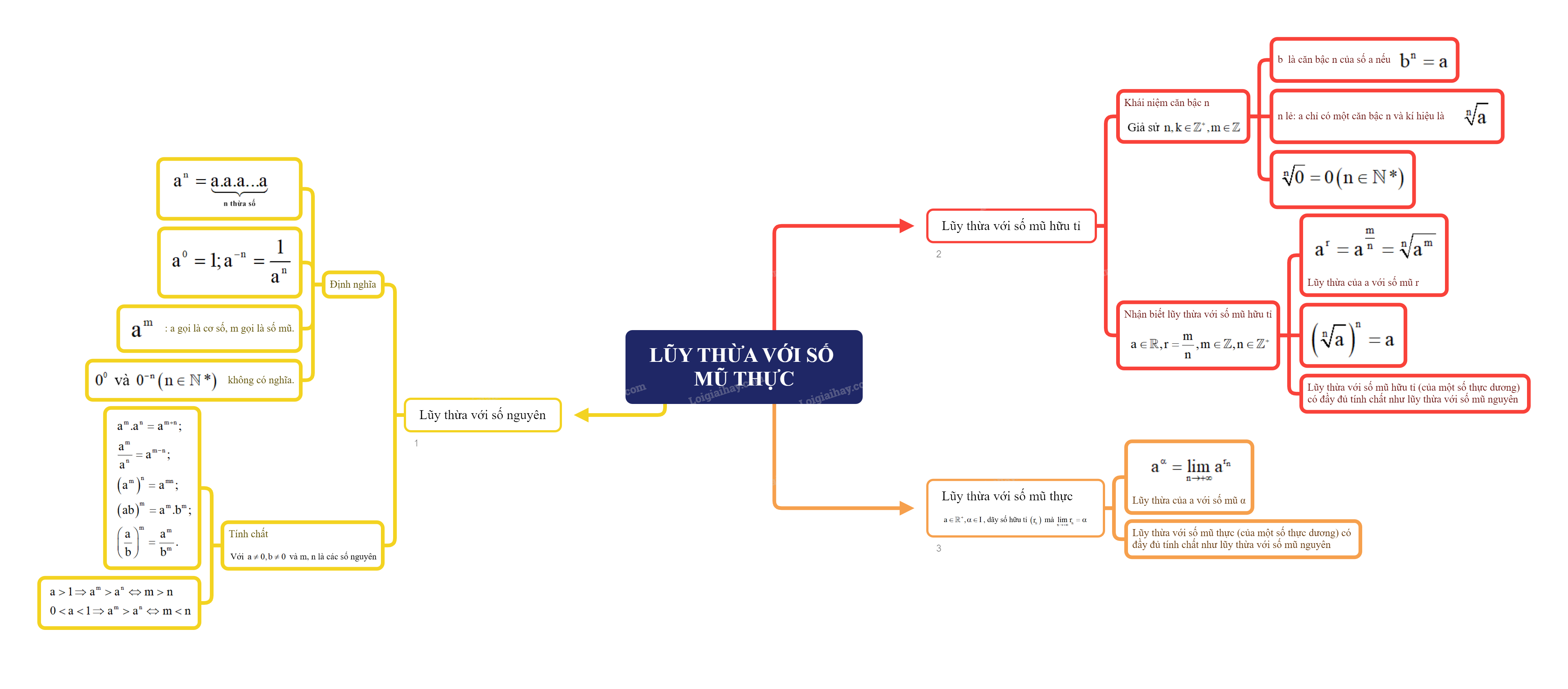
1. Lũy thừa với số mũ nguyên
a) Định nghĩa
- Cho n là một số nguyên dương. Ta định nghĩa:
Với a là số thực tùy ý:
\({a^n} = \underbrace {a.a.a...a}_{n\,thừa\,số}\)
Với a là số thực khác 0:
\({a^0} = 1;{a^{ - n}} = \frac{1}{{{a^n}}}\).
- Trong biểu thức \({a^m}\), a gọi là cơ số, m gọi là số mũ.
Chú ý: \({0^0}\) và \({0^{ - n}}\left( {n \in \mathbb{N}*} \right)\) không có nghĩa.
b) Tính chất
Với \(a \ne 0,b \ne 0\) và m, n là các số nguyên, ta có:
\(\begin{array}{l}{a^m}.{a^n} = {a^{m + n}};\\\frac{{{a^m}}}{{{a^n}}} = {a^{m - n}};\\{\left( {{a^m}} \right)^n} = {a^{mn}};\\{\left( {ab} \right)^m} = {a^m}.{b^m};\\{\left( {\frac{a}{b}} \right)^m} = \frac{{{a^m}}}{{{b^m}}}.\end{array}\)
Chú ý:
- Nếu \(a > 1\) thì \({a^m} > {a^n}\) khi và chỉ khi m > n.
- Nếu \(0 < a < 1\) thì \({a^m} > {a^n}\) khi và chỉ khi m < n.
2. Lũy thừa với số mũ hữu tỉ
a) Khái niệm căn bậc n
Cho số thực a và số nguyên dương n. Số b được gọi là căn bậc n của số a nếu \({b^n} = a\).
Nhận xét: Khi n là số lẻ, mỗi số thực a chỉ có một căn bậc n và kí hiệu là \(\sqrt[n]{a}\) (gọi là căn số học bậc n của a), giá trị âm kí hiệu là \( - \sqrt[n]{a}\).
Chú ý: \(\sqrt[n]{0} = 0\left( {n \in \mathbb{N}*} \right)\).
b) Tính chất của căn bậc n
Giả sử n, k là các số nguyên dương, m là số nguyên. Khi đó:
\(\sqrt[n]{a}.\sqrt[n]{b} = \sqrt[n]{{ab}}\)
\(\frac{{\sqrt[n]{a}}}{{\sqrt[n]{b}}} = \sqrt[n]{{\frac{a}{b}}}\)
\({\left( {\sqrt[n]{a}} \right)^m} = \sqrt[n]{{{a^m}}}\)
\(\sqrt[n]{{\sqrt[k]{a}}} = \sqrt[{nk}]{a}\)
(Giả thiết các biểu thức ở trên đều có nghĩa).
c) Nhận biết lũy thừa với số mũ hữu tỉ
Cho số thực a và số hữu tỉ \(r = \frac{m}{n}\), trong đó m là một số nguyên và n là một số nguyên dương. Lũy thừa của a với số mũ r, kí hiệu là \({a^r}\), xác định bởi \({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\).
Lưu ý: \({\left( {\sqrt[n]{a}} \right)^n} = a\).
Chú ý: Lũy thừa với số mũ hữu tỉ (của một số thực dương) có đầy đủ tính chất như lũy thừa với số mũ nguyên đã nêu trong Mục 1.
3. Lũy thừa với số mũ thực
Cho a là số thực dương và \(\alpha \) là một số vô tỉ. Xét dãy số hữu tỉ \(\left( {{r_n}} \right)\) mà \(\mathop {\lim }\limits_{n \to + \infty } {r_n} = \alpha \). Khi đó, dãy số \(\left( {{a^{{r_n}}}} \right)\) có giới hạn xác định và không phụ thuộc vào dãy số hữu tỉ \(\left( {{r_n}} \right)\) đã chọn. Giới hạn đó gọi là lũy thừa của a với số mũ \(\alpha \), kí hiệu là \({a^\alpha }\).
\({a^\alpha } = \mathop {\lim }\limits_{n \to + \infty } {a^{{r_n}}}\).
Chú ý: Lũy thừa với số mũ thực (của một số thực dương) có đầy đủ tính chất như lũy thừa với số mũ nguyên đã nêu trong Mục 1.
