Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải mục 2 trang 120, 121 SGK Toán 11 tập 1 - Kết nối tri thức
SGK Toán 11 - Kết nối tri thức
Toán 11 tập 1 - Kết nối tri thức với cuộc sống
Chương 5 Giới hạn.Hàm số liên tục
Bài 17. Hàm số liên tục

Giải mục 2 trang 120, 121 SGK Toán 11 tập 1 - Kết nối tri thức

Giải mục 2 trang 120, 121 SGK Toán 11 tập 1 - Kết nối tri thức

Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 11 tập 1 - Kết nối tri thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tốt nhất để giúp bạn học tập hiệu quả.

Bài viết này sẽ tập trung vào việc giải mục 2 trang 120, 121, giúp bạn hiểu rõ các khái niệm và phương pháp giải bài tập liên quan.

Cho hai hàm số (fleft( x right) = left{ {begin{array}{*{20}{c}}{2x;,;0 le x le frac{1}{2}}{1;,frac{1}{2} < x le 1}end{array}} right.) và (gleft( x right) = left{ {begin{array}{*{20}{c}}{x;,0 le x le frac{1}{2}}{1;,frac{1}{2} < x le 1}end{array}} right.)

HĐ 2LT 2

HĐ 2

    Video hướng dẫn giải

    Cho hai hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{2x\;,\;0 \le x \le \frac{1}{2}}\\{1\;,\frac{1}{2} < x \le 1}\end{array}} \right.\) và \(g\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{x\;,0 \le x \le \frac{1}{2}}\\{1\;,\frac{1}{2} < x \le 1}\end{array}} \right.\)với đồ thị tương ứng như Hình 5.7

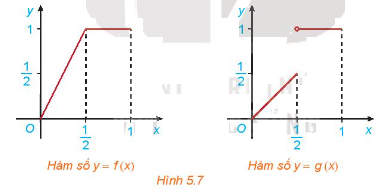
    Giải mục 2 trang 120, 121 SGK Toán 11 tập 1 - Kết nối tri thức 1

    Xét tính liên tục của các hàm số f(x) và g(x) tại điểm \(x = \frac{1}{2}\)và nhận xét về sự khác nhau giữa hai đồ thị.

    Phương pháp giải:

    Hàm số \(f\left( x \right)\) liên tục trên khoảng \(\left( {a,b} \right)\) nếu nó liên tục tại mọi điểm thuộc khoảng này

    Hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {a,b} \right]\) nếu nó liên tục trên khoảng \(\left( {a,b} \right)\) và

     \(\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = f\left( a \right),\;\) \(\mathop {\lim }\limits_{x \to {b^ - }} f\left( x \right) = f\left( b \right)\)

    Lời giải chi tiết:

    \(\mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ - }} 2x = 1\)

    \(\mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ + }} 1 = 1\)

    \(f\left( {\frac{1}{2}} \right) = 1\)

    Vậy \(f\left( x \right)\) liên tục tại \(x = \frac{1}{2}\)

    \(\mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ - }} g\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ - }} x = \frac{1}{2}\)

    \(\mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ - }} 1 = 1\)

    \(g\left( {\frac{1}{2}} \right) = \frac{1}{2}\)

    Vậy \(g\left( x \right)\) gián đoạn tại \(x = \frac{1}{2}\)

    Đồ thị \(f\left( x \right)\) liên tục trên đoạn \(\left[ {0;1} \right],\) đồ thị \(g\left( x \right)\) bị gián đoạn tại \(x = \frac{1}{2}\)

    LT 2

      Video hướng dẫn giải

      Tìm các khoảng trên đó hàm số \(f\left( x \right) = \frac{{{x^2} + 1}}{{x + 2}}\) liên tục.

      Phương pháp giải:

      Hàm phân thức liên tục trên tập xác định.

      Lời giải chi tiết:

      Tập xác định của \(f\left( x \right)\) là \(\left( { - \infty ;\; - 2} \right) \cup \left( { - 2;\; + \infty } \right)\)

      Vây hàm số \(f\left( x \right)\) liên tục trên các khoảng \(\left( { - \infty ; - 2} \right);\left( { - 2; + \infty } \right)\).

      Giải mục 2 trang 120, 121 SGK Toán 11 tập 1 - Kết nối tri thức: Tổng quan và Phương pháp giải

      Mục 2 trong SGK Toán 11 tập 1 - Kết nối tri thức thường xoay quanh các chủ đề về Hàm số bậc hai, bao gồm định nghĩa, tính chất, đồ thị và ứng dụng của hàm số này. Việc nắm vững kiến thức về hàm số bậc hai là nền tảng quan trọng cho các chương trình học toán ở các lớp trên.

      Nội dung chính của Mục 2 trang 120, 121

      • Định nghĩa hàm số bậc hai: Hàm số bậc hai có dạng y = ax2 + bx + c, với a ≠ 0.
      • Hệ số a và tính chất của đồ thị: Hệ số a quyết định độ lồi hoặc lõm của đồ thị parabol. Nếu a > 0, đồ thị hướng lên trên; nếu a < 0, đồ thị hướng xuống dưới.
      • Đỉnh của parabol: Tọa độ đỉnh của parabol là I(x0; y0), với x0 = -b/2a và y0 = f(x0).
      • Trục đối xứng của parabol: Đường thẳng x = x0 là trục đối xứng của parabol.
      • Tìm nghiệm của phương trình bậc hai: Phương trình ax2 + bx + c = 0 có nghiệm khi và chỉ khi biệt thức Δ = b2 - 4ac ≥ 0.

      Giải chi tiết các bài tập trong Mục 2 trang 120, 121

      Dưới đây là giải chi tiết một số bài tập tiêu biểu trong Mục 2 trang 120, 121 SGK Toán 11 tập 1 - Kết nối tri thức:

      Bài 1: Xác định hệ số a, b, c của hàm số y = 2x2 - 5x + 3

      Giải: Trong hàm số y = 2x2 - 5x + 3, ta có a = 2, b = -5, c = 3.

      Bài 2: Tìm đỉnh và trục đối xứng của parabol y = -x2 + 4x - 1

      Giải:

      1. Tính x0 = -b/2a = -4/(2*(-1)) = 2
      2. Tính y0 = f(x0) = f(2) = -(2)2 + 4(2) - 1 = 3
      3. Vậy đỉnh của parabol là I(2; 3) và trục đối xứng là x = 2.

      Bài 3: Giải phương trình 3x2 + 2x - 1 = 0

      Giải:

      1. Tính Δ = b2 - 4ac = 22 - 4(3)(-1) = 16
      2. Vì Δ > 0, phương trình có hai nghiệm phân biệt:
      3. x1 = (-b + √Δ) / 2a = (-2 + 4) / (2*3) = 1/3
      4. x2 = (-b - √Δ) / 2a = (-2 - 4) / (2*3) = -1

      Mẹo giải nhanh các bài tập về hàm số bậc hai

      Để giải nhanh các bài tập về hàm số bậc hai, bạn có thể áp dụng một số mẹo sau:

      • Sử dụng công thức tính đỉnh và trục đối xứng: Việc nắm vững công thức này giúp bạn tiết kiệm thời gian tính toán.
      • Phân tích biệt thức Δ: Dựa vào dấu của Δ, bạn có thể xác định số nghiệm của phương trình bậc hai.
      • Sử dụng các tính chất của hàm số bậc hai: Ví dụ, nếu a > 0, hàm số đạt giá trị nhỏ nhất tại đỉnh; nếu a < 0, hàm số đạt giá trị lớn nhất tại đỉnh.

      Luyện tập thêm

      Để củng cố kiến thức và kỹ năng giải bài tập về hàm số bậc hai, bạn nên luyện tập thêm với các bài tập khác trong SGK và các tài liệu tham khảo. tusach.vn sẽ tiếp tục cập nhật thêm nhiều lời giải chi tiết và bài tập luyện tập để hỗ trợ bạn trong quá trình học tập.

      Chúc bạn học tốt!

      Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

      CHỦ ĐỀ SÁCH XEM NHIỀU

      Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

      VỀ TUSACH.VN