Giải Mục 3 Trang 91 SGK Toán 11 Tập 1 - Kết Nối Tri Thức
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 11 Tập 1 - Kết Nối Tri Thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tốt nhất để giúp bạn học tập hiệu quả.
Bài giải Mục 3 trang 91 này sẽ giúp bạn nắm vững kiến thức và kỹ năng cần thiết để giải quyết các bài toán tương tự.
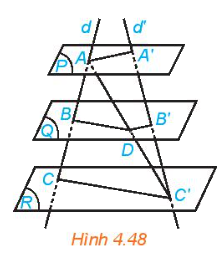
Cho mặt phẳng (P), (Q) và (R) đôi một song song. Hai đường thẳng phân biệt d và d’ cắt ba mặt phẳng lần lượt tại A, B, C và A’, B’, C’ (C khác C’). Gọi D là giao điểm của AC’ và (Q) (H.4.48)
a) Các cặp đường thẳng BD và CC’, B’D và AA’ có song song với nhau không?
b) Các tỉ số (frac{{AB}}{{BC}},frac{{AD}}{{DC'}}) và (frac{{A'B'}}{{B'C'}}) có bằng nhau không?
Giải Mục 3 Trang 91 SGK Toán 11 Tập 1 - Kết Nối Tri Thức: Chi Tiết và Dễ Hiểu
Mục 3 trang 91 SGK Toán 11 Tập 1 - Kết Nối Tri Thức thường xoay quanh các bài toán về đường thẳng và mặt phẳng trong không gian. Nội dung này là nền tảng quan trọng cho việc học tập các kiến thức hình học không gian ở các lớp trên. Do đó, việc nắm vững các khái niệm và phương pháp giải quyết các bài toán liên quan là vô cùng cần thiết.
Nội dung chính của Mục 3 trang 91
Mục 3 thường bao gồm các dạng bài tập sau:
- Xác định vị trí tương đối giữa đường thẳng và mặt phẳng: Bài tập yêu cầu xác định đường thẳng song song, vuông góc, cắt mặt phẳng, hoặc nằm trong mặt phẳng.
- Tính góc giữa đường thẳng và mặt phẳng: Sử dụng định nghĩa và công thức tính góc để tìm góc cần tìm.
- Tính khoảng cách từ một điểm đến mặt phẳng: Áp dụng công thức tính khoảng cách và các định lý liên quan.
- Chứng minh các đẳng thức hình học: Sử dụng các tính chất của đường thẳng và mặt phẳng để chứng minh các đẳng thức.
Phương pháp giải bài tập hiệu quả
Để giải quyết các bài tập trong Mục 3 trang 91 một cách hiệu quả, bạn cần:
- Nắm vững các định nghĩa và tính chất: Hiểu rõ các khái niệm về đường thẳng, mặt phẳng, vị trí tương đối, góc, khoảng cách.
- Sử dụng các công thức một cách chính xác: Áp dụng đúng công thức tính góc, khoảng cách, và các công thức liên quan.
- Vẽ hình minh họa: Vẽ hình giúp bạn hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
- Phân tích bài toán: Xác định các yếu tố đã cho và yếu tố cần tìm, từ đó lựa chọn phương pháp giải phù hợp.
Ví dụ minh họa (giả định một bài tập cụ thể)
Bài tập: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).
Giải:
- Vì SA vuông góc với mặt phẳng (ABCD) nên SA vuông góc với AC.
- Trong tam giác SAC vuông tại A, ta có: tan(góc SCA) = SA/AC = a/(a√2) = 1/√2.
- Vậy, góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng góc SCA, và góc SCA = arctan(1/√2).
Lưu ý quan trọng
Khi giải các bài tập về đường thẳng và mặt phẳng, bạn cần chú ý đến các trường hợp đặc biệt, chẳng hạn như:
- Đường thẳng vuông góc với mặt phẳng.
- Đường thẳng song song với mặt phẳng.
- Hai mặt phẳng vuông góc.
Tusach.vn – Hỗ trợ học tập Toán 11 hiệu quả
Tusach.vn cung cấp đầy đủ lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 11 Tập 1 - Kết Nối Tri Thức. Chúng tôi luôn cập nhật nội dung mới nhất và cung cấp các bài tập tương tự để bạn luyện tập và củng cố kiến thức. Hãy truy cập tusach.vn ngay hôm nay để học tập hiệu quả hơn!
Bảng tóm tắt công thức (ví dụ)
| Công thức | Mô tả |
|---|
| Góc giữa đường thẳng d và mặt phẳng (P) | sin(θ) = d(A, (P)) / AD (A thuộc d, AD thuộc (P)) |
| Khoảng cách từ điểm A đến mặt phẳng (P) | d(A, (P)) = |MA.n| / ||n|| (M thuộc (P), n là vector pháp tuyến của (P)) |
