Giải mục 3 trang 46, 47 SGK Toán 11 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải Mục 3 Trang 46, 47 SGK Toán 11 Tập 2 - Kết Nối Tri Thức
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 11 tập 2 - Kết Nối Tri Thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, đặc biệt là với những bài tập đòi hỏi tư duy và vận dụng kiến thức.
Bài viết này sẽ tập trung vào việc giải Mục 3 trang 46, 47, giúp bạn hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Cho hai mặt phẳng (P) và (Q) vuông góc với nhau.
HĐ3
Video hướng dẫn giải
Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Kẻ đường thẳng a thuộc (P) và vuông góc với giao tuyến \(\Delta \) của (P) và (Q). Gọi O là giao điểm của a và \(\Delta \). Trong mặt phẳng (Q), gọi b là đường thẳng vuông góc với \(\Delta \) tại O.
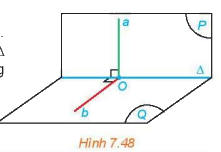
a) Tính góc giữa a và b.
b) Tìm mỗi quan hệ giữa a và (Q).
Phương pháp giải:
- Sử dụng nhận xét trang 45 để xác định góc giữa 2 mặt phẳng.
- Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó.
Lời giải chi tiết:
a) \(\left\{ \begin{array}{l}(P) \cap (Q) = \Delta \\a \subset (P),a \bot \Delta \\b \subset (Q),b \bot \Delta \end{array} \right. \Rightarrow \left( {(P),(Q)} \right) = \left( {a,b} \right)\)
Do \((P) \bot (Q) \Rightarrow \left( {(P),(Q)} \right) = {90^0} \Rightarrow \left( {a,b} \right) = {90^0}\)
b) Do \(\left\{ \begin{array}{l}a \bot b\\a \bot \Delta \\b \cap \Delta \end{array} \right. \Rightarrow a \bot (Q)\)
HĐ4
Video hướng dẫn giải
Cho hai mặt phẳng (P) và (Q) cắt nhau theo giao tuyến a và cùng vuông góc với mặt phẳng (R). Gọi O là một điểm thuộc a và a' là đường thẳng qua O và vuông góc với (R).

a) Hỏi a' có nằm trong các mặt phẳng (P), (Q) hay không?
b) Tìm mối quan hệ giữa a và a'.
c) Tìm mối quan hệ giữa a và (R).
Phương pháp giải:
Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Mỗi đường thẳng qua điểm O thuộc (P) và vuông góc với mặt phẳng (Q) thì đường thẳng đó thuộc mặt phẳng (P).
Lời giải chi tiết:
a) Vì O là một điểm thuộc a là giao tuyến của hai mặt phẳng (P), (Q) và a' là đường thẳng qua O và vuông góc với (R).
Theo nhận xét trang 46 thì a' có nằm trong các mặt phẳng (P), (Q).
b) Vì a' có nằm trong các mặt phẳng (P), (Q) nên a’ là giao tuyến của hai mặt phẳng (P), (Q) do đó a trùng a' (do a cũng là giao tuyến của hai mặt phẳng (P), (Q)).
c) a vuông góc với (R) do a trùng a’ và a’ vuông góc với (R).
LT3
Video hướng dẫn giải
Với giả thiết như ở Ví dụ 3, chứng minh rằng:
a) Các mặt phẳng (AB'C'D') và (ABCD) cùng vuông góc với (SAC);
b) Giao tuyển của hai mặt phẳng (AB'C'D') và (ABCD) là đường thẳng đi qua A, nằm trong mặt phẳng (ABCD) và vuông góc với AC.
Phương pháp giải:
Nếu hai mặt phẳng cắt nhau và cùng vuông góc với một mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.
Lời giải chi tiết:

a) Từ ví dụ 3b ta có AB’, AC’ cùng đi qua A và vuông góc với SC
\( \Rightarrow SC \bot \left( {AB'C'D'} \right),SC \subset \left( {SAC} \right) \Rightarrow \left( {AB'C'D'} \right) \bot \left( {SAC} \right)\)
Ta có \(SA \bot \left( {ABCD} \right),SA \subset \left( {SAC} \right) \Rightarrow \left( {ABCD} \right) \bot \left( {SAC} \right)\)
Do đó các mặt phẳng (AB'C'D') và (ABCD) cùng vuông góc với (SAC).
b) Vì (AB'C'D') và (ABCD) cùng vuông góc với (SAC) nên giao tuyến của hai mặt phẳng (AB'C'D') và (ABCD) vuông góc với (SAC)
Vậy giao tuyển của hai mặt phẳng (AB'C'D') và (ABCD) là đường thẳng đi qua A, nằm trong mặt phẳng (ABCD) và vuông góc với AC.
Giải Mục 3 Trang 46, 47 SGK Toán 11 Tập 2 - Kết Nối Tri Thức: Hướng Dẫn Chi Tiết
Mục 3 trong SGK Toán 11 tập 2 - Kết Nối Tri Thức thường xoay quanh các chủ đề về đạo hàm của hàm số, bao gồm các quy tắc tính đạo hàm, đạo hàm của các hàm số cơ bản và ứng dụng của đạo hàm trong việc giải các bài toán liên quan đến cực trị, khoảng đơn điệu của hàm số. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương trình Toán học ở các lớp trên.
Nội Dung Chính Của Mục 3
- Đạo hàm của hàm số: Định nghĩa đạo hàm, ý nghĩa hình học và vật lý của đạo hàm.
- Quy tắc tính đạo hàm: Quy tắc tính đạo hàm của tổng, hiệu, tích, thương của các hàm số.
- Đạo hàm của các hàm số cơ bản: Đạo hàm của hàm số lũy thừa, hàm số mũ, hàm số logarit, hàm số lượng giác và hàm số ngược của chúng.
- Ứng dụng của đạo hàm: Giải các bài toán tìm cực trị, khoảng đơn điệu của hàm số, và các bài toán liên quan đến tối ưu hóa.
Giải Chi Tiết Bài Tập Trang 46, 47
Dưới đây là lời giải chi tiết cho các bài tập trong Mục 3 trang 46, 47 SGK Toán 11 tập 2 - Kết Nối Tri Thức:
Bài 1: (Trang 46)
Đề bài: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Lời giải:
f'(x) = 3x2 + 4x - 5
Bài 2: (Trang 46)
Đề bài: Tính đạo hàm của hàm số g(x) = sin(x) + cos(x).
Lời giải:
g'(x) = cos(x) - sin(x)
Bài 3: (Trang 47)
Đề bài: Tìm đạo hàm của hàm số h(x) = ex + ln(x).
Lời giải:
h'(x) = ex + 1/x
Mẹo Giải Bài Tập Đạo Hàm Hiệu Quả
- Nắm vững các quy tắc tính đạo hàm: Đây là nền tảng cơ bản để giải các bài tập về đạo hàm.
- Phân tích cấu trúc hàm số: Xác định hàm số là tổng, hiệu, tích hay thương của các hàm số khác để áp dụng quy tắc phù hợp.
- Sử dụng bảng đạo hàm của các hàm số cơ bản: Giúp tiết kiệm thời gian và tránh sai sót.
- Kiểm tra lại kết quả: Đảm bảo rằng kết quả đạo hàm của bạn là chính xác.
Ứng Dụng Của Đạo Hàm Trong Thực Tế
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
- Vật lý: Tính vận tốc, gia tốc của vật chuyển động.
- Kinh tế: Tính chi phí biên, doanh thu biên, lợi nhuận biên.
- Kỹ thuật: Tối ưu hóa thiết kế, điều khiển hệ thống.
Hy vọng rằng với hướng dẫn chi tiết này, bạn đã có thể giải thành công các bài tập trong Mục 3 trang 46, 47 SGK Toán 11 tập 2 - Kết Nối Tri Thức. Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại liên hệ với chúng tôi tại tusach.vn để được hỗ trợ.
| Hàm số | Đạo hàm |
|---|---|
| f(x) = xn | f'(x) = nxn-1 |
| f(x) = sin(x) | f'(x) = cos(x) |
| f(x) = cos(x) | f'(x) = -sin(x) |