Lý thuyết Giá trị lượng giác của góc lượng giác - SGK Toán 11 Kết nối tri thức
Tổng quan nội dung
Lý thuyết Giá trị lượng giác của góc lượng giác - Toán 11 Kết nối tri thức
Bài viết này cung cấp đầy đủ và chi tiết lý thuyết về giá trị lượng giác của góc lượng giác, thuộc chương trình SGK Toán 11 Kết nối tri thức. Chúng ta sẽ cùng nhau tìm hiểu về định nghĩa, tính chất, và các công thức quan trọng liên quan đến sin, cosin, tang, cotang của một góc lượng giác.
Nội dung được trình bày một cách dễ hiểu, kèm theo ví dụ minh họa giúp học sinh nắm bắt kiến thức một cách nhanh chóng và hiệu quả. Đây là tài liệu học tập không thể thiếu cho các em học sinh lớp 11 đang ôn tập và chuẩn bị cho các kỳ thi.
1. Góc lượng giác
a, Khái niệm góc lượng giác và số đo của góc lượng giác
Trong mặt phẳng, cho 2 tia Ou, Ov. Xét tia Om cùng nằm tròn mặt phẳng này. Nếu tia Om quay quanh điểm O, theo một chiều nhất định từ Ou đến Ov, thì ta nói nó quét một góc lượng giác với tia đầu Ou và tia cuối Ov.
Kí hiệu: (Ou, Ov).
Số đo của góc lượng giác có tia đầu Ou và tia cuối Ov kí hiệu là sđ(Ou, Ov).

b, Hệ thức Chasles
Với 3 tia Ou, Ov, Ow bất kì ta có:
Sđ(Ou,Ov) + sđ(Ov, Ow) = sđ(Ou,Ow) +k360o.
2. Đơn vị đo góc và độ dài cung tròn
a, Đơn vị đo góc và cung tròn
Đơn vị độ: \({1^o} = 60',1' = 60''\)
Đơn vị rađian: \({1^o} = \frac{\pi }{{180}}\)rad, 1 rad =\({\left( {\frac{{180}}{\pi }} \right)^o}\)
b, Độ dài cung tròn
Một cung tròn của đường tròn bán kính R và có số đo \(\alpha \)rad thì có độ dài \(l = R\alpha \)
3. Giá trị lượng giác của góc lượng giác
a, Đường tròn lượng giác
Đường tròn lượng giác là đường tròn có tâm tại gốc tọa độ, bán kính bằng 1, được định hướng và lấy điểm A(1;0) làm điểm gốc của đường tròn.
Điểm trên đường tròn lượng giác biểu diễn góc lượng giác có số đo \(\alpha \)(độ hoặc rad) là điểm M trên đường tròn lượng giác sao cho sđ (OA, OM) =\(\alpha \).
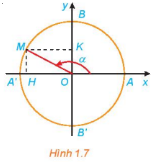
b, Các giá trị lượng giác của góc lượng giác:
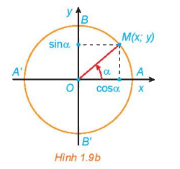
Trục tung là trục sin, trục hoành là trục côsin
Điểm M(x;y) nằm trên đường tròn như hình vẽ. Khi đó:
\(x = \)cos\(\alpha \), \(y = \)sin\(\alpha \).
tan\(\alpha \)\( = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{y}{x}\left( {x \ne 0} \right)\)
\(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{x}{y}\left( {y \ne 0} \right)\).
c, Bảng xác định dấu của các giá trị lượng giác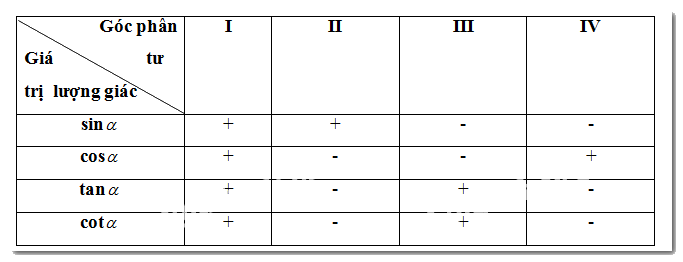
d, Giá trị lượng giác của các góc đặc biệt
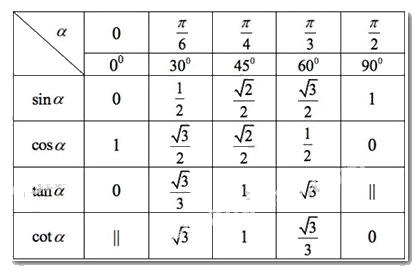
e, Cách bấm máy tính để tìm giá trị lượng giác của góc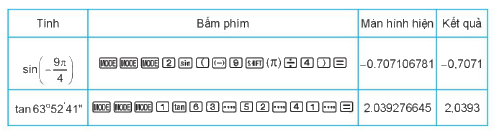
4. Quan hệ giữa các giá trị lượng giác
a, Các công thức lượng giác cơ bản
\(\begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\left( {\alpha \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right)\\1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\left( {\alpha \ne k\pi ,k \in \mathbb{Z}} \right)\\\tan \alpha .\cot \alpha = 1\left( {\alpha \ne \frac{{k\pi }}{2},k \in \mathbb{Z}} \right)\end{array}\)
b, Giá trị lượng giác của các góc có liên quan đặc biệt (cos đối, sin bù, phụ chéo, khác pi tan)
- Góc đối nhau (\(\alpha \) và - \(\alpha \))
\(\begin{array}{l}\sin \left( { - \alpha } \right) = - \sin \alpha \\\cos \left( { - \alpha } \right) = \cos \alpha \\\tan \left( { - \alpha } \right) = - \tan \alpha \\\cot \left( { - \alpha } \right) = - \cot \alpha \end{array}\)
- Góc bù nhau (\(\alpha \) và \(\pi \) - \(\alpha \))
\(\begin{array}{l}\sin \left( {\pi - \alpha } \right) = \sin \alpha \\\cos \left( {\pi - \alpha } \right) = - \cos \alpha \\\tan \left( {\pi - \alpha } \right) = - \tan \alpha \\\cot \left( {\pi - \alpha } \right) = - \cot \alpha \end{array}\)
- Góc phụ nhau (\(\alpha \) và \(\frac{\pi }{2}\) - \(\alpha \))
\(\begin{array}{l}\sin \left( {\frac{\pi }{2} - \alpha } \right) = c{\rm{os}}\alpha \\\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \\\tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \\\cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \end{array}\)
- Góc hơn kém \(\pi \) (\(\alpha \) và \(\pi \) + \(\alpha \))
\(\begin{array}{l}\sin \left( {\pi + \alpha } \right) = - \sin \alpha \\\cos \left( {\pi + \alpha } \right) = - \cos \alpha \\\tan \left( {\pi + \alpha } \right) = \tan \alpha \\\cot \left( {\pi + \alpha } \right) = \cot \alpha \end{array}\)
Lý Thuyết Giá Trị Lượng Giác của Góc Lượng Giác - SGK Toán 11 Kết Nối Tri Thức
Chào mừng các em học sinh lớp 11 đến với bài học về Lý thuyết Giá trị lượng giác của góc lượng giác, một phần quan trọng trong chương trình SGK Toán 11 Kết nối tri thức. Bài viết này sẽ cung cấp cho các em một cái nhìn tổng quan và chi tiết về chủ đề này, giúp các em nắm vững kiến thức nền tảng và tự tin giải quyết các bài tập liên quan.
1. Góc Lượng Giác và Số Đo Cung
Trước khi đi sâu vào giá trị lượng giác, chúng ta cần hiểu rõ về góc lượng giác và số đo cung. Một góc lượng giác được xác định bởi một đường tròn lượng giác và một điểm trên đường tròn đó. Số đo cung là độ dài cung trên đường tròn đơn vị, thường được đo bằng radian hoặc độ.
- Độ: Một vòng tròn đầy đủ là 360 độ.
- Radian: Một vòng tròn đầy đủ là 2π radian.
Công thức chuyển đổi giữa độ và radian: radian = (độ * π) / 180
2. Định Nghĩa Giá Trị Lượng Giác
Trên đường tròn lượng giác đơn vị (bán kính bằng 1), với điểm M(x, y) là điểm cuối của cung AM có số đo α, ta định nghĩa các giá trị lượng giác của góc α như sau:
- Sin (sin α): y (tung độ của điểm M)
- Cosin (cos α): x (hoành độ của điểm M)
- Tang (tan α): sin α / cos α = y / x (với x ≠ 0)
- Cotang (cot α): cos α / sin α = x / y (với y ≠ 0)
3. Tính Chất và Dấu của Giá Trị Lượng Giác
Giá trị lượng giác của một góc có thể dương, âm hoặc bằng không, tùy thuộc vào vị trí của điểm M trên đường tròn lượng giác. Dưới đây là bảng tóm tắt dấu của các giá trị lượng giác theo các góc phần tư:
| Góc phần tư | sin α | cos α | tan α | cot α |
|---|---|---|---|---|
| I (0° - 90°) | + | + | + | + |
| II (90° - 180°) | + | - | - | - |
| III (180° - 270°) | - | - | + | + |
| IV (270° - 360°) | - | + | - | - |
4. Giá Trị Lượng Giác của Các Góc Đặc Biệt
Một số góc đặc biệt có giá trị lượng giác quen thuộc mà các em cần nhớ:
- sin 0° = 0, cos 0° = 1, tan 0° = 0, cot 0° = ∞
- sin 90° = 1, cos 90° = 0, tan 90° = ∞, cot 90° = 0
- sin 180° = 0, cos 180° = -1, tan 180° = 0, cot 180° = ∞
- sin 270° = -1, cos 270° = 0, tan 270° = ∞, cot 270° = 0
- sin 360° = 0, cos 360° = 1, tan 360° = 0, cot 360° = ∞
5. Các Công Thức Lượng Giác Cơ Bản
Có rất nhiều công thức lượng giác, nhưng một số công thức cơ bản mà các em cần nắm vững bao gồm:
- sin2 α + cos2 α = 1
- tan α = sin α / cos α
- cot α = cos α / sin α
- 1 + tan2 α = 1 / cos2 α
- 1 + cot2 α = 1 / sin2 α
6. Bài Tập Vận Dụng
Để củng cố kiến thức, các em hãy thử giải các bài tập sau:
- Tính giá trị của sin 30°, cos 45°, tan 60°.
- Cho α là góc nhọn. Biết sin α = 0.6, hãy tính cos α và tan α.
- Chứng minh đẳng thức: sin4 α + cos4 α = 1 - 2sin2 α cos2 α.
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về Lý thuyết Giá trị lượng giác của góc lượng giác. Chúc các em học tập tốt!