Đề bài
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại \(B,BC = \) a và \(\widehat {CAB} = {30^0}\). Biết \(SA \bot (ABC)\) và \(SA = a\sqrt 2 \).
a) Chứng minh rằng \((SBC) \bot (SAB)\).
b) Tính theo a khoảng cách từ điểm \(A\) đến đường thẳng SC và khoảng cách từ điểm \(A\) đến mặt phẳng \((SBC)\).
Phương pháp giải - Xem chi tiết
- Hai mặt phẳng được gọi là vuông góc nếu một đường thẳng nằm trong mặt phẳng này vuông góc với mặt phẳng kia.
- Khoảng cách từ một điểm M đến một đường thẳng a là khoảng cách giữa M và hình chiếu H của M trên a.
- Khoảng cách từ một điểm M đến một mặt phẳng (P) là khoảng cách giữa M và hình chiếu H của M trên (P).
Lời giải chi tiết
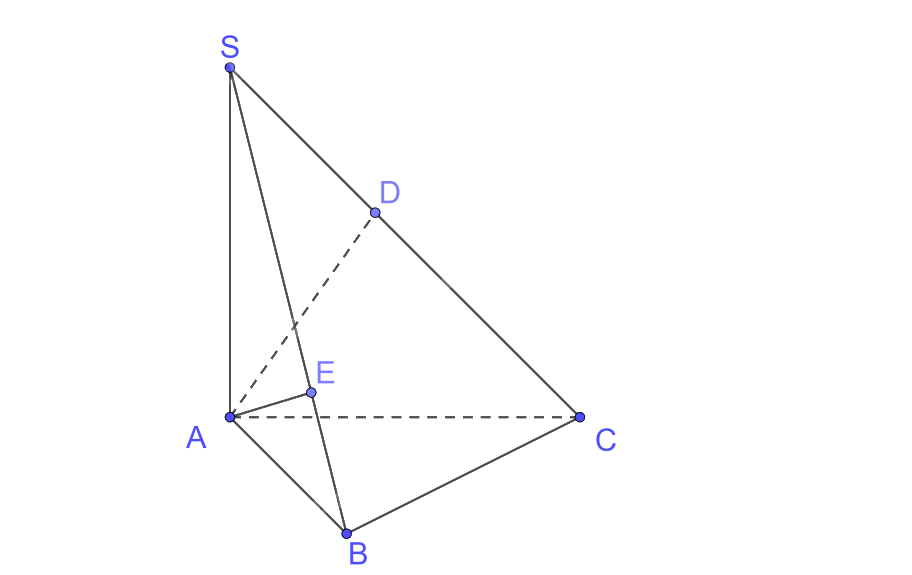
a) \(SA \bot BC\left( {SA \bot \left( {ABC} \right)} \right),AB \bot BC \Rightarrow BC \bot \left( {SAB} \right),BC \subset \left( {SBC} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right)\)
b) +) Trong (SAC) kẻ \(AD \bot SC \Rightarrow d\left( {A,SC} \right) = AD\)
Xét tam giác ABC vuông tại B có
\(\sin \widehat {CAB} = \frac{{BC}}{{AC}} \Rightarrow AC = \frac{a}{{\sin {{30}^0}}} = 2a\)
Xét tam giác SAC vuông tại A có
\(\frac{1}{{A{D^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {2a} \right)}^2}}} = \frac{3}{{4{a^2}}} \Rightarrow AD = \frac{{2a\sqrt 3 }}{3}\)
Do đó \(d\left( {A,SC} \right) = \frac{{2a\sqrt 3 }}{3}\)
+) \(\left( {SAB} \right) \bot \left( {SBC} \right),\left( {SAB} \right) \cap \left( {SBC} \right) = SB\)
Trong (SAB) kẻ \(AE \bot SB\)
\( \Rightarrow AE \bot \left( {SBC} \right) \Rightarrow d\left( {A,\left( {SBC} \right)} \right) = AE\)
Xét tam giác ABC vuông tại B có
\(\tan \widehat {CAB} = \frac{{BC}}{{AB}} \Rightarrow AB = \frac{a}{{\tan {{30}^0}}} = a\sqrt 3 \)
Xét tam giác SAB vuông tại A có
\(\frac{1}{{A{E^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {a\sqrt 3 } \right)}^2}}} = \frac{5}{{6{a^2}}} \Rightarrow AE = \frac{{a\sqrt {30} }}{5}\)
Vậy \(d\left( {A,\left( {SBC} \right)} \right) = \frac{{a\sqrt {30} }}{5}\)
