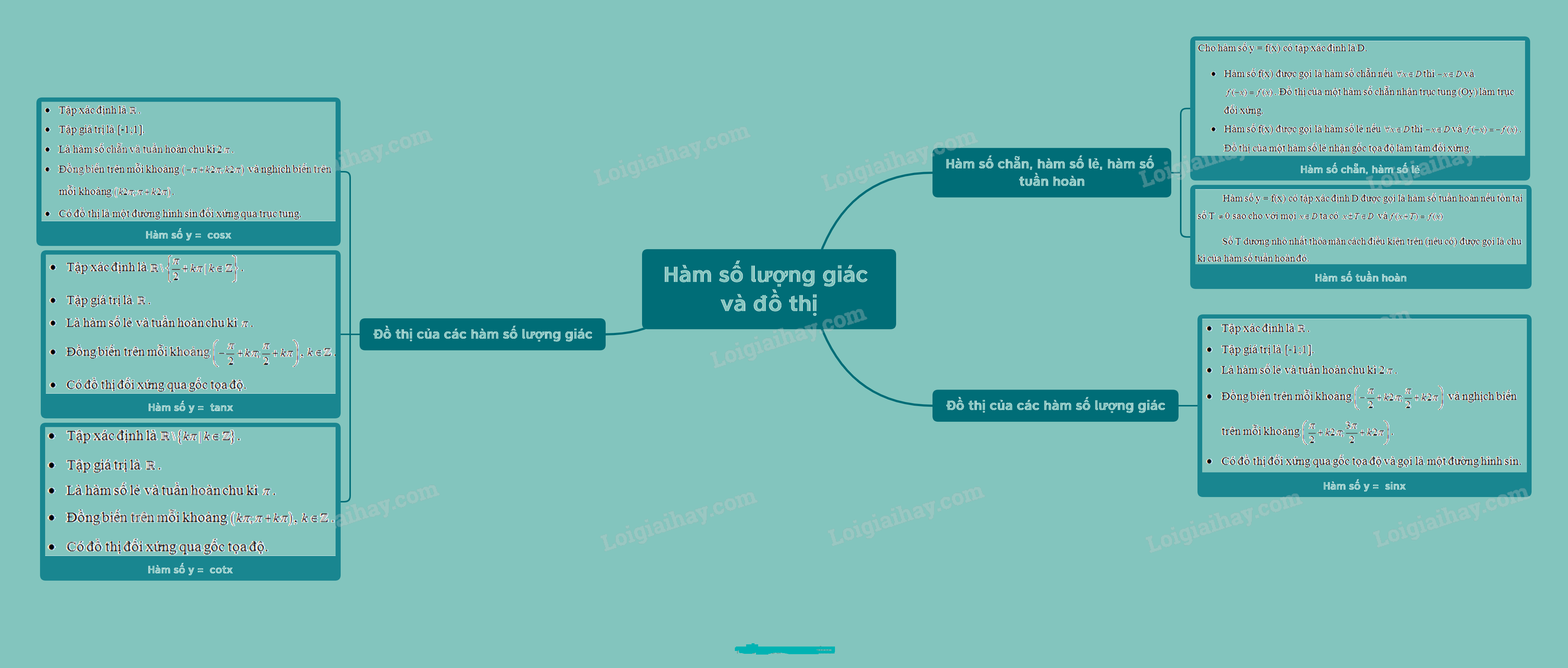
Lý Thuyết Hàm Số Lượng Giác - Toán 11 Kết Nối Tri Thức: Tổng Quan Chi Tiết
Hàm số lượng giác đóng vai trò then chốt trong chương trình Toán 11 Kết nối tri thức, là cầu nối giữa hình học và đại số. Bài viết này sẽ cung cấp một cái nhìn toàn diện về lý thuyết hàm số lượng giác, bao gồm định nghĩa, tính chất, đồ thị và ứng dụng.
1. Góc Lượng Giác và Đơn Vị Đo Góc
Trước khi đi sâu vào hàm số lượng giác, chúng ta cần hiểu rõ về góc lượng giác và đơn vị đo góc. Góc lượng giác được định nghĩa bằng một đường tròn lượng giác, với điểm gốc là tâm đường tròn, điểm đầu là điểm A trên đường tròn và điểm cuối là điểm M trên đường tròn.
- Đơn vị độ (°): Một vòng tròn được chia thành 360 độ.
- Đơn vị radian (rad): Một vòng tròn có độ dài cung bằng bán kính. 1 radian ≈ 57.3 độ.
2. Hàm Số Lượng Giác Cơ Bản
Có bốn hàm số lượng giác cơ bản:
- Sin (sin x): Tỷ số giữa cạnh đối và cạnh huyền trong tam giác vuông.
- Cosin (cos x): Tỷ số giữa cạnh kề và cạnh huyền trong tam giác vuông.
- Tang (tan x): Tỷ số giữa cạnh đối và cạnh kề trong tam giác vuông.
- Cotang (cot x): Tỷ số giữa cạnh kề và cạnh đối trong tam giác vuông.
Các hàm số lượng giác này được định nghĩa trên đường tròn lượng giác và có các tính chất đặc biệt.
3. Giá Trị Lượng Giác của Các Góc Đặc Biệt
Việc nắm vững giá trị lượng giác của các góc đặc biệt (0°, 30°, 45°, 60°, 90°) là rất quan trọng để giải các bài toán lượng giác một cách nhanh chóng và chính xác.
| Góc (x) | sin x | cos x | tan x | cot x |
|---|
| 0° | 0 | 1 | 0 | Không xác định |
| 30° | 1/2 | √3/2 | 1/√3 | √3 |
| 45° | √2/2 | √2/2 | 1 | 1 |
| 60° | √3/2 | 1/2 | √3 | 1/√3 |
| 90° | 1 | 0 | Không xác định | 0 |
4. Các Công Thức Lượng Giác Cơ Bản
Có rất nhiều công thức lượng giác hữu ích, bao gồm:
- sin2x + cos2x = 1
- tan x = sin x / cos x
- cot x = cos x / sin x
- Công thức cộng và hiệu góc
- Công thức nhân đôi
Việc thành thạo các công thức này sẽ giúp bạn giải quyết các bài toán phức tạp hơn.
5. Đồ Thị Hàm Số Lượng Giác
Đồ thị hàm số lượng giác giúp chúng ta hiểu rõ hơn về tính chất của hàm số, như chu kỳ, biên độ, và giá trị lớn nhất, giá trị nhỏ nhất.
Ví dụ, đồ thị hàm số y = sin x là một đường cong tuần hoàn với chu kỳ 2π.
6. Ứng Dụng của Hàm Số Lượng Giác
Hàm số lượng giác có rất nhiều ứng dụng trong thực tế, bao gồm:
- Vật lý: Mô tả các hiện tượng dao động, sóng.
- Kỹ thuật: Tính toán các góc, khoảng cách trong xây dựng, hàng không.
- Địa lý: Xác định vị trí, đo đạc khoảng cách trên bản đồ.
Kết luận:
Lý thuyết hàm số lượng giác là một phần quan trọng của chương trình Toán 11 Kết nối tri thức. Hy vọng bài viết này đã cung cấp cho bạn một cái nhìn tổng quan và chi tiết về chủ đề này. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải các bài toán thực tế.