Bài 3.2 trang 61 SGK Toán 11 tập 1 - Kết nối tri thức
Tổng quan nội dung
Bài 3.2 trang 61 SGK Toán 11 Tập 1 - Kết Nối Tri Thức
Bài 3.2 trang 61 SGK Toán 11 Tập 1 thuộc chương 1: Hàm số và đồ thị. Bài học này tập trung vào việc tìm tập xác định của hàm số, một kiến thức nền tảng quan trọng trong chương trình Toán 11.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu cùng với các ví dụ minh họa giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải bài tập.
Số sản phẩm một công nhân làm được trong một ngày được cho như sau: 18 25 39 12 54 27 46 25 19 9 36 22 20 19 17 44 5 18 23 28 25 34 46 27 16 Hãy chuyển mẫu số liệu sang dạng ghép nhóm với sau nhóm có độ dài bằng nhau
Đề bài
Số sản phẩm một công nhân làm được trong một ngày được cho như sau:
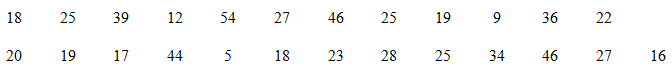
Hãy chuyển mẫu số liệu sang dạng ghép nhóm với sáu nhóm có độ dài bằng nhau.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Để chuyển mẫu số liệu không ghép nhóm sang mẫu số liệu ghép nhóm, ta làm như sau:
Bước 1: Chia miền giá trị của mẫu số liệu thành một số nhóm theo tiêu chí cho trước.
Bước 2: Đếm số giá trị của mẫu số liệu thuộc mỗi nhóm (tần số) và lập bảng thống kê cho mẫu số liệu ghép.
Lời giải chi tiết
Giá trị nhỏ nhất là: 5.
Giá trị lớn nhất là 54.
Do đó khoảng biến thiên là 54 - 5 = 49.
Để chia thành 6 nhóm với độ dài bằng nhau ta lấy điểm đầu mút phải trái của nhóm đầu tiên là 3 và đầu mút phải của nhóm cuối cùng là 57 với độ dài mỗi nhóm là 9.
Ta được mẫu số liệu ghép nhóm như sau:

Bài 3.2 Trang 61 SGK Toán 11 Tập 1 - Kết Nối Tri Thức: Giải Chi Tiết và Hướng Dẫn
Bài 3.2 trang 61 SGK Toán 11 Tập 1 - Kết Nối Tri Thức yêu cầu học sinh tìm tập xác định của các hàm số đã cho. Đây là một bài tập quan trọng giúp củng cố kiến thức về điều kiện xác định của hàm số, đặc biệt là các hàm số chứa căn thức, phân thức và logarit.
1. Lý Thuyết Nền Tảng
Trước khi đi vào giải bài tập, chúng ta cần nắm vững các kiến thức sau:
- Tập xác định của hàm số: Là tập hợp tất cả các giá trị của x sao cho hàm số f(x) có nghĩa.
- Điều kiện xác định của các hàm số thường gặp:
- Hàm căn thức: Biểu thức dưới dấu căn phải lớn hơn hoặc bằng 0.
- Hàm phân thức: Mẫu số khác 0.
- Hàm logarit: Cơ số phải lớn hơn 0 và khác 1, biểu thức trong logarit phải lớn hơn 0.
2. Giải Bài 3.2 Trang 61 SGK Toán 11 Tập 1 - Kết Nối Tri Thức
Dưới đây là lời giải chi tiết cho từng câu của bài tập 3.2:
Câu a)
Hàm số: y = √(2x - 1)
Điều kiện xác định: 2x - 1 ≥ 0
Giải bất phương trình: 2x ≥ 1 => x ≥ 1/2
Vậy tập xác định của hàm số là: D = [1/2; +∞)
Câu b)
Hàm số: y = 1 / (x - 3)
Điều kiện xác định: x - 3 ≠ 0
Giải phương trình: x ≠ 3
Vậy tập xác định của hàm số là: D = ℝ \ {3}
Câu c)
Hàm số: y = log2(x + 2)
Điều kiện xác định: x + 2 > 0
Giải bất phương trình: x > -2
Vậy tập xác định của hàm số là: D = (-2; +∞)
3. Luyện Tập Thêm
Để nắm vững hơn về cách tìm tập xác định của hàm số, bạn có thể luyện tập thêm với các bài tập sau:
- Tìm tập xác định của hàm số y = √(4 - x2)
- Tìm tập xác định của hàm số y = log3(x2 - 4)
4. Lưu Ý Quan Trọng
Khi tìm tập xác định của hàm số, hãy luôn kiểm tra kỹ các điều kiện xác định của từng loại hàm số thành phần. Việc bỏ qua bất kỳ điều kiện nào có thể dẫn đến kết quả sai.
5. Kết Luận
Bài 3.2 trang 61 SGK Toán 11 Tập 1 - Kết Nối Tri Thức là một bài tập cơ bản nhưng quan trọng trong việc củng cố kiến thức về tập xác định của hàm số. Hy vọng với lời giải chi tiết và hướng dẫn trên, các bạn học sinh có thể tự tin giải bài tập và nắm vững kiến thức này.
Chúc các bạn học tốt!