Bài 11 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức
Tổng quan nội dung
Bài 11 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức
Bài 11 thuộc chương trình Toán 11 tập 2, tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Bài tập này yêu cầu học sinh vận dụng kiến thức về các hàm số lượng giác cơ bản, tính chất của chúng và các phương pháp giải phương trình lượng giác.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và (SA bot (ABC),SA = asqrt 2 ).
Đề bài
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và \(SA \bot (ABC),SA = a\sqrt 2 \). Khoảng cách từ \(A\) đến mặt phẳng \((SBC)\) bằng
A. \(\frac{{6a}}{{11}}\).
B. \(\frac{{a\sqrt {66} }}{{11}}\).
C. \(\frac{{a\sqrt 6 }}{{11}}\).
D. \(\frac{{a\sqrt {11} }}{{11}}\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Khoảng cách từ một điểm M đến một mặt phẳng (P) là khoảng cách giữa M và hình chiếu H của M trên (P)
Lời giải chi tiết
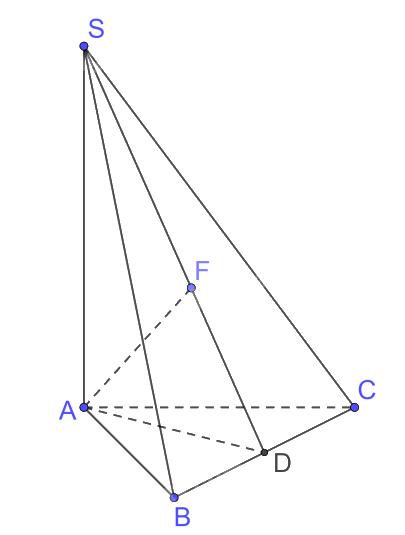
Trong (ABC) kẻ \(AD \bot BC\)
Mà tam giác ABC đều cạnh a nên \(AD = \frac{{a\sqrt 3 }}{2}\)
Ta có \(SA \bot BC,AD \bot BC \Rightarrow BC \bot \left( {SAD} \right);BC \subset \left( {SBC} \right) \Rightarrow \left( {SAD} \right) \bot \left( {SBC} \right)\)
Mà \(\left( {SAD} \right) \cap \left( {SBC} \right) = SD\)
Trong (SAD) kẻ \(AF \bot SD\)
Do đó \(AF \bot \left( {SBC} \right) \Rightarrow d\left( {A,\left( {SBC} \right)} \right) = AF\)
Xét tam giác SAD có
\(\frac{1}{{A{F^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{D^2}}} = \frac{1}{{{{\left( {a\sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}} = \frac{{11}}{{6{a^2}}} \Rightarrow AF = \frac{{\sqrt {66} }}{{11}}a\)
Vậy \(d\left( {A,\left( {SBC} \right)} \right) = \frac{{a\sqrt {66} }}{{11}}\)
Đáp án B
Bài 11 trang 106 SGK Toán 11 Tập 2 - Kết Nối Tri Thức: Giải Chi Tiết và Hướng Dẫn
Bài 11 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức là một bài tập quan trọng trong chương trình ôn tập chương 3 về hàm số lượng giác. Bài tập này giúp học sinh củng cố kiến thức về các hàm số lượng giác, các phép biến đổi lượng giác và phương pháp giải phương trình lượng giác. Dưới đây là giải chi tiết bài 11, kèm theo hướng dẫn và các lưu ý quan trọng.
Nội dung bài tập
Bài 11 yêu cầu học sinh giải các phương trình lượng giác sau:
- a) sin(x) = 1/2
- b) cos(x) = -√3/2
- c) tan(x) = 1
- d) cot(x) = 0
Giải chi tiết
a) sin(x) = 1/2
Phương trình sin(x) = 1/2 có nghiệm là:
- x = π/6 + k2π (k ∈ Z)
- x = 5π/6 + k2π (k ∈ Z)
Giải thích: Hàm sin có giá trị 1/2 tại góc π/6 và 5π/6 trong khoảng [0, 2π). Do tính tuần hoàn của hàm sin, ta cộng thêm k2π để được nghiệm tổng quát.
b) cos(x) = -√3/2
Phương trình cos(x) = -√3/2 có nghiệm là:
- x = 5π/6 + k2π (k ∈ Z)
- x = 7π/6 + k2π (k ∈ Z)
Giải thích: Hàm cos có giá trị -√3/2 tại góc 5π/6 và 7π/6 trong khoảng [0, 2π).
c) tan(x) = 1
Phương trình tan(x) = 1 có nghiệm là:
- x = π/4 + kπ (k ∈ Z)
Giải thích: Hàm tan có giá trị 1 tại góc π/4 trong khoảng [0, π). Do tính tuần hoàn của hàm tan, ta cộng thêm kπ để được nghiệm tổng quát.
d) cot(x) = 0
Phương trình cot(x) = 0 có nghiệm là:
- x = π/2 + kπ (k ∈ Z)
Giải thích: Hàm cot có giá trị 0 tại góc π/2 trong khoảng [0, π). Do tính tuần hoàn của hàm cot, ta cộng thêm kπ để được nghiệm tổng quát.
Lưu ý quan trọng
- Khi giải phương trình lượng giác, cần xác định đúng khoảng nghiệm và nghiệm tổng quát.
- Nắm vững các giá trị lượng giác đặc biệt của các góc thường gặp (0, π/6, π/4, π/3, π/2, π, 3π/2, 2π).
- Sử dụng các công thức lượng giác để biến đổi phương trình về dạng đơn giản hơn.
- Kiểm tra lại nghiệm để đảm bảo tính chính xác.
Ứng dụng thực tế
Các kiến thức về hàm số lượng giác và phương trình lượng giác có ứng dụng rộng rãi trong nhiều lĩnh vực như:
- Vật lý: Mô tả các hiện tượng dao động, sóng.
- Kỹ thuật: Xử lý tín hiệu, điều khiển tự động.
- Địa lý: Tính toán góc phương vị, độ cao.
Kết luận: Bài 11 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số lượng giác và phương trình lượng giác. Việc nắm vững kiến thức và kỹ năng giải bài tập này sẽ giúp học sinh học tốt môn Toán 11 và áp dụng vào thực tế.
Mọi thắc mắc về bài tập, vui lòng liên hệ tusach.vn để được hỗ trợ!