Bài 13 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức
Tổng quan nội dung
Bài 13 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức
Bài 13 thuộc chương trình Toán 11 tập 2, sách Kết nối tri thức, tập trung vào việc ôn tập chương 3: Hàm số lượng giác. Bài học này giúp học sinh củng cố kiến thức về các hàm số lượng giác cơ bản, các phép biến đổi lượng giác và ứng dụng của chúng trong giải toán.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu cho từng bài tập trong Bài 13, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho tứ diện đều ABCD có cạnh bằng (a). Gọi M, N lần lượt là trung điểm của cạnh AC và cạnh AD.
Đề bài
Cho tứ diện đều ABCD có cạnh bằng \(a\). Gọi M, N lần lượt là trung điểm của cạnh AC và cạnh AD. Thể tích khối chóp \(B\).CMND bằng
A. \(\frac{{{a^3}\sqrt 2 }}{{12}}\)
B. \(\frac{{{a^3}\sqrt 2 }}{{16}}\).
C. \(\frac{{{a^3}\sqrt 2 }}{{24}}\).
D. \(\frac{{{a^3}\sqrt 2 }}{8}\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Thể tích khối chóp đều cạnh a: \(V = \frac{{\sqrt 2 {a^3}}}{{12}}\)
- Tỉ lệ thể tích: \(\frac{{{V_{S.ABC}}}}{{{V_{S.A'B'C'}}}} = \frac{{SA}}{{SA'}}.\frac{{SB}}{{SB'}}.\frac{{SC}}{{SC'}}\)
Lời giải chi tiết
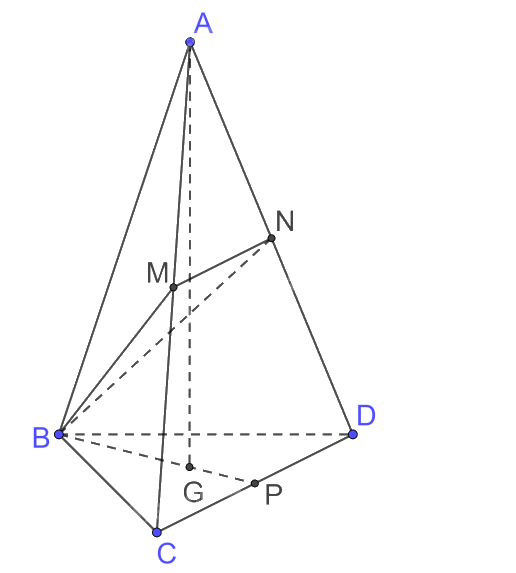
Thể tích khối chóp đều cạnh a: \(V = \frac{{\sqrt 2 {a^3}}}{{12}}\)
Ta có \(\frac{{{V_{A.BMN}}}}{{{V_{A.BCD}}}} = \frac{{AB}}{{AB}}.\frac{{AM}}{{AC}}.\frac{{AN}}{{AD}} = \frac{1}{2}.\frac{1}{2} = \frac{1}{4}\)
Mà \({V_{A.BCD}} = {V_{A.BMN}} + {V_{B.CMND}}\)
\( \Rightarrow {V_{B.CMND}} = \frac{3}{4}{V_{ABCD}} = \frac{3}{4}.\frac{{\sqrt 2 {a^3}}}{{12}} = \frac{{\sqrt 2 {a^3}}}{{16}}\)
Đáp án B
Bài 13 trang 106 SGK Toán 11 Tập 2 - Kết Nối Tri Thức: Giải Chi Tiết & Lời Giải
Chào mừng các em học sinh đến với lời giải chi tiết Bài 13 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức. Bài học này là phần ôn tập chương 3, đòi hỏi các em nắm vững kiến thức về hàm số lượng giác, các công thức biến đổi và ứng dụng của chúng.
I. Tổng Quan Về Bài 13 Toán 11 Tập 2 - Kết Nối Tri Thức
Bài 13 tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến:
- Xác định tập xác định của hàm số lượng giác.
- Tìm tập giá trị của hàm số lượng giác.
- Giải phương trình lượng giác cơ bản.
- Chứng minh các đẳng thức lượng giác.
- Ứng dụng hàm số lượng giác vào giải các bài toán thực tế.
II. Lời Giải Chi Tiết Các Bài Tập Trong Bài 13
Dưới đây là lời giải chi tiết cho từng bài tập trong Bài 13 trang 106 SGK Toán 11 tập 2 - Kết nối tri thức:
Bài 13.1 Trang 106 Toán 11 Tập 2
(Đề bài: ... - Ví dụ về một bài tập cụ thể)
Lời giải:
(Giải thích chi tiết từng bước giải bài tập, kèm theo các công thức và lý thuyết liên quan)
Bài 13.2 Trang 106 Toán 11 Tập 2
(Đề bài: ... - Ví dụ về một bài tập cụ thể)
Lời giải:
(Giải thích chi tiết từng bước giải bài tập, kèm theo các công thức và lý thuyết liên quan)
III. Các Công Thức Lượng Giác Quan Trọng Cần Nhớ
Để giải tốt các bài tập trong chương này, các em cần nắm vững các công thức lượng giác sau:
| Công thức | Mô tả |
|---|---|
| sin2x + cos2x = 1 | Công thức lượng giác cơ bản |
| tan x = sin x / cos x | Hệ thức giữa tan, sin và cos |
| cot x = cos x / sin x | Hệ thức giữa cot, sin và cos |
IV. Mẹo Giải Bài Tập Lượng Giác Hiệu Quả
Để giải các bài tập lượng giác một cách hiệu quả, các em có thể áp dụng một số mẹo sau:
- Sử dụng các công thức biến đổi lượng giác để đưa phương trình về dạng đơn giản hơn.
- Chú ý đến điều kiện xác định của hàm số lượng giác.
- Kiểm tra lại kết quả sau khi giải xong.
V. Luyện Tập Thêm
Để củng cố kiến thức, các em có thể luyện tập thêm các bài tập tương tự trong sách bài tập hoặc trên các trang web học toán trực tuyến.
tusach.vn hy vọng với lời giải chi tiết và những hướng dẫn trên, các em sẽ học tốt môn Toán 11 và đạt kết quả cao trong các kỳ thi sắp tới. Chúc các em thành công!