Giải mục 1 trang 44, 45 SGK Toán 11 tập 2 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho mục 1 trang 44, 45 sách giáo khoa Toán 11 tập 2 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em học sinh hiểu rõ các khái niệm, định lý và phương pháp giải bài tập liên quan.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và đầy đủ nhất để hỗ trợ quá trình học tập của các em.
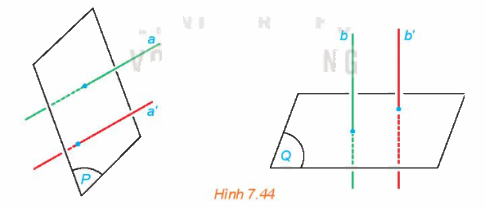
Cho hai mặt phẳng (P) và (Q). Lấy hai đường thẳng a, a' cùng vuông góc với (P)
Giải mục 1 trang 44, 45 SGK Toán 11 tập 2 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 1 trang 44, 45 SGK Toán 11 tập 2 - Kết nối tri thức tập trung vào việc ôn tập chương 3: Hàm số lượng giác và ứng dụng của hàm số lượng giác. Nội dung chính bao gồm các dạng bài tập về xác định tính đơn điệu, giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác, giải phương trình lượng giác cơ bản và ứng dụng vào các bài toán thực tế.
Nội dung chi tiết các bài tập trong mục 1
Mục 1 bao gồm các bài tập từ 1 đến 6, mỗi bài tập đều có những yêu cầu và độ khó khác nhau. Dưới đây là phân tích chi tiết từng bài:
Bài 1: Tính đơn điệu của hàm số lượng giác
Bài 1 yêu cầu học sinh xác định khoảng đồng biến, nghịch biến của các hàm số lượng giác như sin, cos, tan, cot. Để giải bài này, cần nắm vững kiến thức về đạo hàm của các hàm số lượng giác và sử dụng dấu của đạo hàm để xác định tính đơn điệu.
Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số lượng giác
Bài 2 tập trung vào việc tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số lượng giác. Phương pháp giải thường sử dụng các công thức lượng giác, đánh giá và sử dụng bất đẳng thức.
Bài 3, 4, 5: Giải phương trình lượng giác cơ bản
Các bài tập từ 3 đến 5 yêu cầu học sinh giải các phương trình lượng giác cơ bản như sin(x) = a, cos(x) = a, tan(x) = a, cot(x) = a. Cần nắm vững các công thức nghiệm của các phương trình lượng giác này và chú ý đến điều kiện xác định của phương trình.
Bài 6: Ứng dụng hàm số lượng giác vào bài toán thực tế
Bài 6 thường là một bài toán ứng dụng thực tế, yêu cầu học sinh sử dụng kiến thức về hàm số lượng giác để giải quyết. Ví dụ, bài toán có thể liên quan đến việc tính chiều cao của một tòa nhà, khoảng cách giữa hai điểm, hoặc góc tạo bởi một đường thẳng và trục hoành.
Phương pháp giải bài tập hiệu quả
- Nắm vững kiến thức lý thuyết: Hiểu rõ các định nghĩa, định lý, công thức lượng giác là nền tảng để giải bài tập.
- Phân tích đề bài: Đọc kỹ đề bài, xác định rõ yêu cầu và các dữ kiện đã cho.
- Lựa chọn phương pháp giải phù hợp: Tùy thuộc vào từng dạng bài, lựa chọn phương pháp giải phù hợp nhất.
- Kiểm tra lại kết quả: Sau khi giải xong, kiểm tra lại kết quả để đảm bảo tính chính xác.
Lời khuyên khi học tập
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Sử dụng tài liệu tham khảo: Tham khảo thêm các sách giáo khoa, tài liệu ôn tập, và các trang web học tập trực tuyến.
- Hỏi thầy cô giáo: Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo để được hướng dẫn và giải đáp.
Bảng tổng hợp công thức lượng giác quan trọng
| Công thức | Mô tả |
|---|
| sin2(x) + cos2(x) = 1 | Công thức lượng giác cơ bản |
| tan(x) = sin(x) / cos(x) | Công thức tính tan(x) |
| cot(x) = cos(x) / sin(x) | Công thức tính cot(x) |
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ tự tin hơn khi giải các bài tập trong mục 1 trang 44, 45 SGK Toán 11 tập 2 - Kết nối tri thức. Chúc các em học tập tốt!
