Giải mục 5 trang 28, 29 SGK Toán 11 tập 1 - Kết nối tri thức

Chào mừng các em học sinh đến với lời giải chi tiết mục 5 trang 28, 29 sách giáo khoa Toán 11 tập 1 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em hiểu rõ hơn về nội dung bài học và tự tin giải các bài tập liên quan.

tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.

Cho hàm số \(y = \tan x\) a) Xét tính chẵn, lẻ của hàm số

Hoạt động 6

Cho hàm số \(y = \tan x\)

a) Xét tính chẵn, lẻ của hàm số

b) Hoàn thành bảng giá trị của hàm số \(y = \tan x\) trên khoảng\(\;\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).

\(x\)	\( - \frac{\pi }{3}\)	\( - \frac{\pi }{4}\)	\( - \frac{\pi }{6}\)	0	\(\frac{\pi }{6}\)	\(\frac{\pi }{4}\)	\(\frac{\pi }{3}\)
\(y = \tan x\)	?	?	?	?	?	?	?

Bằng cách lấy nhiều điểm \(M\left( {x;\tan x} \right)\) với \(x \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) và nối lại ta được đồ thị hàm số \(y = \tan x\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\).

c) Bằng cách làm tương tự câu b cho các đoạn khác có độ dài bằng chu kỳ \(T = \pi \), ta được đồ thị của hàm số \(y = \tan x\) như hình dưới đây.

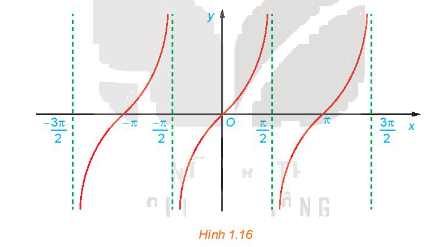
Giải mục 5 trang 28, 29 SGK Toán 11 tập 1 - Kết nối tri thức 1

Từ đồ thị ở Hình 1.16, hãy tìm tập giá trị và các khoảng đồng biến của hàm số \(y = \tan x\).

Phương pháp giải:

Sử dụng định nghĩa hàm số chẵn lẻ

Dựa vào đồ thị để xác định tập giá trị, các khoảng đồng biến, nghịch biến của hàm số.

Lời giải chi tiết:

a) Tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ {\frac{\pi }{2} + k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\)

Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D

Ta có: \(f\left( { - x} \right) = \tan \left( { - x} \right) = - \tan x = - f\left( x \right),\;\forall x\; \in \;D\)

Vậy \(y = \tan x\) là hàm số lẻ.

\(x\)	\( - \frac{\pi }{3}\)	\( - \frac{\pi }{4}\)	\( - \frac{\pi }{6}\)	\(0\)	\(\frac{\pi }{6}\)	\(\frac{\pi }{4}\)	\(\frac{\pi }{3}\)
\(\tan x\)	\( - \sqrt 3 \)	\( - 1\)	\( - \frac{{\sqrt 3 }}{3}\)	\(0\)	\(\frac{{\sqrt 3 }}{3}\)	\(1\)	\(\sqrt 3 \)

c) Từ đồ thị trên, ta thấy hàm số \(y = \tan x\) có tập xác định là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi {\rm{|}}\;k\; \in \;\mathbb{Z}} \right\}\), tập giá trị là \(\mathbb{R}\) và đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\).

Luyện tập

Sử dụng đồ thị đã vẽ ở Hình 1.16, hãy xác định các giá trị của x trên đoạn \(\left[ { - \pi ;\frac{{3\pi }}{2}} \right]\) để hàm số \(y = \tan x\) nhận giá trị âm.

Phương pháp giải:

Nhìn đồ thị để xác định vị trí của y và x

Lời giải chi tiết:

Hàm số nhận giá trị âm ứng với phần đồ thị nằm dưới trục hoành. Từ đồ thị ta suy ra trên đoạn \(\left[ { - \pi ;\frac{{3\pi }}{2}} \right]\), thì \(y < 0\) khi \(x\; \in \left( { - \frac{\pi }{2};0} \right) \cup \left( {\frac{\pi }{2};\;\pi } \right)\)

Giải mục 5 trang 28, 29 SGK Toán 11 tập 1 - Kết nối tri thức: Tổng quan và Phương pháp giải

Mục 5 trang 28, 29 SGK Toán 11 tập 1 - Kết nối tri thức tập trung vào việc ôn tập chương 1: Hàm số và đồ thị. Đây là một phần quan trọng, đặt nền móng cho các kiến thức tiếp theo trong chương trình học. Việc nắm vững các khái niệm, định lý và phương pháp giải bài tập trong mục này là vô cùng cần thiết.

Nội dung chính của Mục 5

Ôn tập về hàm số: Các loại hàm số (hàm số bậc nhất, hàm số bậc hai, hàm số mũ, hàm số logarit), tập xác định, tập giá trị, tính đơn điệu, cực trị.
Đồ thị hàm số: Cách vẽ đồ thị hàm số, các tính chất của đồ thị, ứng dụng của đồ thị trong việc giải quyết các bài toán.
Bài tập vận dụng: Các bài tập tổng hợp giúp học sinh rèn luyện kỹ năng và củng cố kiến thức đã học.

Phương pháp giải bài tập hiệu quả

Để giải tốt các bài tập trong mục 5, các em cần:

Nắm vững lý thuyết: Hiểu rõ các khái niệm, định lý và công thức liên quan đến hàm số và đồ thị.
Phân tích đề bài: Xác định đúng yêu cầu của đề bài, các dữ kiện đã cho và các đại lượng cần tìm.
Lựa chọn phương pháp giải phù hợp: Tùy thuộc vào từng bài tập cụ thể, các em có thể sử dụng các phương pháp như: vẽ đồ thị, sử dụng tính chất của hàm số, giải phương trình, bất phương trình.
Kiểm tra lại kết quả: Sau khi giải xong bài tập, các em nên kiểm tra lại kết quả để đảm bảo tính chính xác.

Giải chi tiết các bài tập trong Mục 5

Dưới đây là giải chi tiết một số bài tập tiêu biểu trong mục 5 trang 28, 29 SGK Toán 11 tập 1 - Kết nối tri thức:

Bài 1: (Trang 28)

(Đề bài)

Giải:

(Giải thích chi tiết từng bước)

Bài 2: (Trang 29)

(Đề bài)

Giải:

(Giải thích chi tiết từng bước)

Lưu ý quan trọng

Trong quá trình giải bài tập, các em cần chú ý:

Sử dụng máy tính bỏ túi khi cần thiết.
Viết rõ ràng, trình bày mạch lạc các bước giải.
Kiểm tra lại các kết quả trung gian và kết quả cuối cùng.

Tài liệu tham khảo thêm

Để học tốt môn Toán 11, các em có thể tham khảo thêm các tài liệu sau:

Sách bài tập Toán 11 tập 1 - Kết nối tri thức.
Các trang web học Toán trực tuyến uy tín.
Các video bài giảng Toán 11 trên YouTube.

Kết luận:

Hy vọng rằng với lời giải chi tiết và phương pháp giải hiệu quả được trình bày trong bài viết này, các em sẽ tự tin hơn khi giải các bài tập trong mục 5 trang 28, 29 SGK Toán 11 tập 1 - Kết nối tri thức. Chúc các em học tập tốt!

Giải mục 5 trang 28, 29 SGK Toán 11 tập 1 - Kết nối tri thức

Giải mục 5 trang 28, 29 SGK Toán 11 tập 1 - Kết nối tri thức

Hoạt động 6

Luyện tập

Giải mục 5 trang 28, 29 SGK Toán 11 tập 1 - Kết nối tri thức: Tổng quan và Phương pháp giải

Nội dung chính của Mục 5

Phương pháp giải bài tập hiệu quả

Giải chi tiết các bài tập trong Mục 5

Bài 1: (Trang 28)

Bài 2: (Trang 29)

Lưu ý quan trọng

Tài liệu tham khảo thêm

CHỦ ĐỀ SÁCH XEM NHIỀU

VỀ TUSACH.VN