Bài 1.3 trang 16 SGK Toán 11 tập 1 - Kết nối tri thức
Tổng quan nội dung
Bài 1.3 trang 16 SGK Toán 11 tập 1 - Kết nối tri thức
Bài 1.3 thuộc chương 1: Hàm số và đồ thị của SGK Toán 11 tập 1 - Kết nối tri thức. Bài học này tập trung vào việc xét tính đơn điệu của hàm số bậc hai. Việc nắm vững kiến thức trong bài sẽ giúp học sinh giải quyết các bài toán liên quan đến hàm số một cách hiệu quả.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu và các bài tập tương tự để giúp bạn hiểu sâu hơn về nội dung bài học.
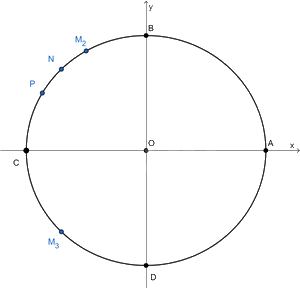
Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau:
Đề bài
Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau:
a) \(\frac{{2\pi }}{3}\); b) \( - \frac{{11\pi }}{4}\); c) \({150^0}\); d) \( - {225^0}\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Để biểu diễn các góc lượng giác trên đường tròn lượng giác ta thường sử dụng các kết quả sau
- Góc \(\alpha \) và góc \(\alpha + k2\pi ,k\; \in \;\mathbb{Z}\) có cùng điểm biểu diễn trên đường tròn lượng giác.
- Số điểm trên đường tròn lượng giác biểu diễn bởi số đo có dạng \(\alpha + \frac{{k2\pi }}{m}\) (với k là số nguyên và m là số nguyên dương). Từ đó để biểu diễn các góc lượng giác đó ta lần lượt cho k từ 0 tới (m – 1) rồi biểu diễn các góc đó.
Lời giải chi tiết
a) Ta có: \(\frac{{\frac{{2\pi }}{3}}}{{2\pi }} = \frac{1}{3}\). Ta chia đường tròn thành 3 phần bằng nhau. Khi đó điểm \({M_2}\) là điểm biểu diễn bởi góc có số đo \(\frac{{2\pi }}{3}\).
b) Ta có \( - \frac{{11\pi }}{4} = - \frac{{3\pi }}{4} + \left( { - 1} \right).2\pi \). Do đó điểm biểu diễn bởi góc \( - \frac{{11\pi }}{4}\) trùng với góc \( - \frac{{3\pi }}{4}\) và là điểm \({M_3}\).
c) Ta có \(\frac{{150}}{{180}} = \frac{5}{6}\). Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó P là điểm biểu diễn bởi góc \({150^0}\)
d) Ta có \( - {225^0} = - {180^0} - {45^0}\). Do đó điểm biểu diễn N là điểm biểu diễn bởi góc \( - {225^0}\)
Bài 1.3 trang 16 SGK Toán 11 tập 1 - Kết nối tri thức: Giải chi tiết và hướng dẫn
Bài 1.3 trang 16 SGK Toán 11 tập 1 - Kết nối tri thức là một bài tập quan trọng trong chương trình học Toán 11, giúp học sinh củng cố kiến thức về hàm số bậc hai và tính đơn điệu của chúng. Dưới đây là giải chi tiết bài tập này, cùng với những hướng dẫn và lưu ý quan trọng để bạn có thể tự giải quyết các bài tập tương tự.
Nội dung bài tập
Bài 1.3 yêu cầu xét tính đơn điệu của các hàm số bậc hai sau:
- a) y = -2x2 + 8x - 5
- b) y = x2 - 4x + 3
- c) y = -x2 + 6x - 9
Phương pháp giải
Để xét tính đơn điệu của hàm số bậc hai y = ax2 + bx + c, ta cần xác định:
- Hệ số a:
- Nếu a > 0: Hàm số đồng biến trên khoảng (-b/2a, +∞) và nghịch biến trên khoảng (-∞, -b/2a).
- Nếu a < 0: Hàm số nghịch biến trên khoảng (-b/2a, +∞) và đồng biến trên khoảng (-∞, -b/2a).
- Đỉnh của parabol: I(-b/2a, -Δ/4a)
Giải chi tiết
a) y = -2x2 + 8x - 5
- a = -2 < 0: Hàm số nghịch biến trên khoảng (-∞, 2) và đồng biến trên khoảng (2, +∞).
- Đỉnh: xI = -b/2a = -8/(-4) = 2
b) y = x2 - 4x + 3
- a = 1 > 0: Hàm số đồng biến trên khoảng (2, +∞) và nghịch biến trên khoảng (-∞, 2).
- Đỉnh: xI = -b/2a = -(-4)/(2*1) = 2
c) y = -x2 + 6x - 9
- a = -1 < 0: Hàm số nghịch biến trên khoảng (3, +∞) và đồng biến trên khoảng (-∞, 3).
- Đỉnh: xI = -b/2a = -6/(-2) = 3
Lưu ý quan trọng
- Luôn xác định hệ số a trước để xác định chiều của parabol.
- Tính tọa độ đỉnh của parabol để xác định khoảng đồng biến, nghịch biến.
- Kiểm tra lại kết quả bằng cách vẽ đồ thị hàm số.
Bài tập tương tự
Để củng cố kiến thức, bạn có thể tự giải các bài tập sau:
- Bài 1.4 trang 16 SGK Toán 11 tập 1 - Kết nối tri thức
- Bài 1.5 trang 17 SGK Toán 11 tập 1 - Kết nối tri thức
tusach.vn hy vọng với lời giải chi tiết và hướng dẫn trên, bạn đã hiểu rõ về Bài 1.3 trang 16 SGK Toán 11 tập 1 - Kết nối tri thức. Chúc bạn học tốt!
| Hàm số | Hệ số a | Tính đơn điệu |
|---|---|---|
| y = -2x2 + 8x - 5 | -2 | Nghịch biến trên (-∞, 2), Đồng biến trên (2, +∞) |
| y = x2 - 4x + 3 | 1 | Nghịch biến trên (-∞, 2), Đồng biến trên (2, +∞) |
| y = -x2 + 6x - 9 | -1 | Đồng biến trên (-∞, 3), Nghịch biến trên (3, +∞) |