Bài 7.39 trang 65 SGK Toán 11 tập 2 - Kết nối tri thức
Tổng quan nội dung
Bài 7.39 trang 65 SGK Toán 11 Tập 2 - Kết Nối Tri Thức
Bài 7.39 thuộc chương trình Toán 11 Tập 2, sách Kết Nối Tri Thức, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự. Hãy cùng khám phá lời giải ngay dưới đây!
Cho tứ diện ABCD có tam giác ABC cân tại (A)
Đề bài
Cho tứ diện ABCD có tam giác ABC cân tại \(A\), tam giác BCD cân tại \(D\). Gọi I là trung điểm của cạnh BC.
a) Chứng minh rằng \(BC \bot (AID)\).
b) Kẻ đường cao AH của tam giác AID. Chứng minh rằng \(AH \bot (BCD)\).
c) Kẻ đường cao IJ của tam giác AID. Chứng minh rằng IJ là đường vuông góc chung của AD và BC.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Đường thẳng vuông góc với mặt phẳng nếu nó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng.
- Hai mặt phẳng vuông góc nếu trong mặt phẳng này có một đường thẳng vuông góc vào giao tuyến thì đường thẳng đó vuông góc với mặt phẳng còn lại.
- Đường thẳng \(\Delta \) cắt hai đường thẳng chéo nhau a, b và vuông góc với cả hai đường thẳng đó được gọi là đường vuông góc chung của a và b.
Lời giải chi tiết
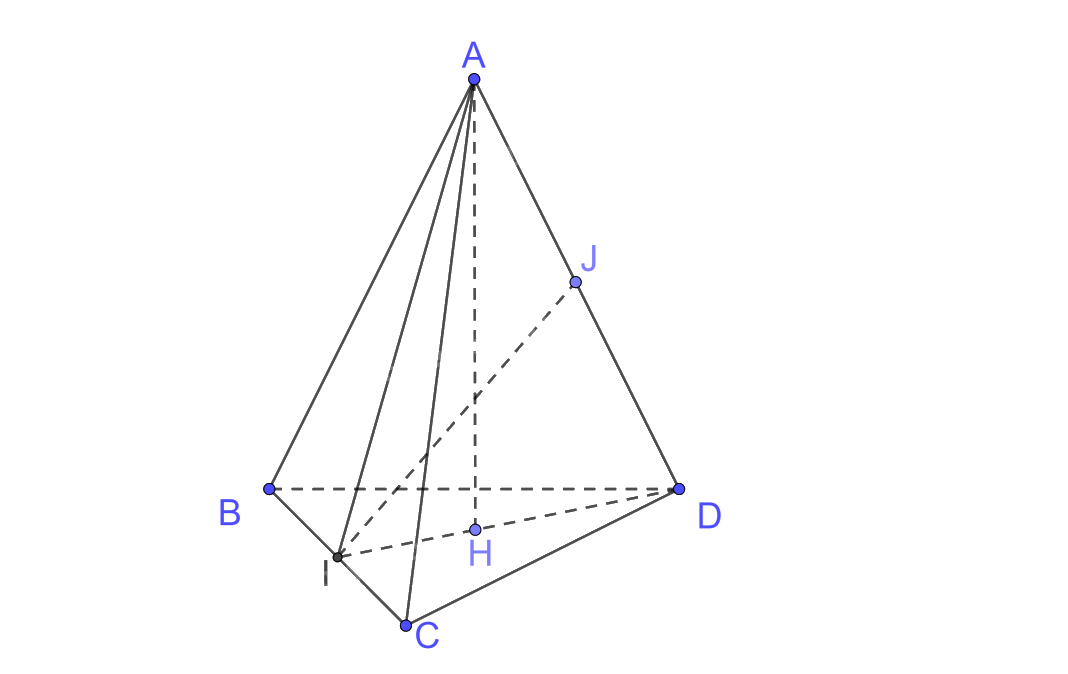
a) Xét tam giác ABC cân tại A có
I là trung điểm của BC
\( \Rightarrow AI \bot BC\)
Xét tam giác ACD cân tại D có
I là trung điểm của BC
\( \Rightarrow DI \bot BC\)
Ta có \(AI \bot BC,DI \bot BC \Rightarrow BC \bot \left( {AID} \right)\)
b) \(BC \bot \left( {AID} \right);BC \subset \left( {BCD} \right) \Rightarrow \left( {BCD} \right) \bot \left( {AID} \right)\)
\(\left( {BCD} \right) \cap \left( {AID} \right) = DI\)
Trong (AID) có \(AH \bot DI\)
\( \Rightarrow AH \bot \left( {BCD} \right)\)
c) Ta có \(BC \bot \left( {AID} \right);IJ \subset \left( {AID} \right) \Rightarrow BC \bot IJ\)
Mà \(IJ \bot AD\)
Do đó IJ là đường vuông góc chung của AD và BC
Bài 7.39 Trang 65 SGK Toán 11 Tập 2 - Kết Nối Tri Thức: Giải Chi Tiết và Hướng Dẫn
Bài 7.39 trang 65 SGK Toán 11 Tập 2 Kết Nối Tri Thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Nội dung bài tập:
Bài tập yêu cầu tìm cực trị của hàm số. Để giải bài tập này, chúng ta cần thực hiện các bước sau:
- Tính đạo hàm cấp một (f'(x)) của hàm số.
- Tìm các điểm dừng (x) bằng cách giải phương trình f'(x) = 0.
- Lập bảng xét dấu f'(x) để xác định khoảng đồng biến, nghịch biến của hàm số.
- Kết luận về cực đại, cực tiểu dựa vào bảng xét dấu f'(x).
Lời giải chi tiết:
(Giả sử hàm số trong bài tập là f(x) = x3 - 3x2 + 2)
- Tính đạo hàm cấp một:
- Tìm các điểm dừng:
- Lập bảng xét dấu f'(x):
- Kết luận:
- Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
- Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
f'(x) = 3x2 - 6x
3x2 - 6x = 0 ⇔ 3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Lưu ý quan trọng:
- Luôn kiểm tra kỹ điều kiện xác định của hàm số trước khi tính đạo hàm.
- Sử dụng đúng các quy tắc tính đạo hàm để tránh sai sót.
- Lập bảng xét dấu đạo hàm một cách cẩn thận để xác định chính xác khoảng đồng biến, nghịch biến và cực trị của hàm số.
Bài tập tương tự:
Để rèn luyện thêm kỹ năng giải bài tập về đạo hàm và ứng dụng của đạo hàm, bạn có thể tham khảo các bài tập tương tự sau:
- Bài 7.40 trang 65 SGK Toán 11 Tập 2 Kết Nối Tri Thức
- Bài 7.41 trang 66 SGK Toán 11 Tập 2 Kết Nối Tri Thức
Tusach.vn – Nguồn tài liệu học tập Toán 11 uy tín:
Tusach.vn là website cung cấp đầy đủ các tài liệu học tập Toán 11, bao gồm:
- Giải bài tập SGK Toán 11 Tập 1, Tập 2
- Bài tập trắc nghiệm Toán 11
- Đề thi thử Toán 11
- Các bài viết hướng dẫn giải Toán 11
Hãy truy cập tusach.vn để học tập và ôn luyện Toán 11 hiệu quả!