Bài 7.19 Trang 53 SGK Toán 11 Tập 2 - Kết Nối Tri Thức

Bài 7.19 trang 53 SGK Toán 11 tập 2 - Kết nối tri thức

Bài 7.19 trang 53 SGK Toán 11 Tập 2 - Kết Nối Tri Thức

Bài 7.19 thuộc chương trình Toán 11 Tập 2, sách Kết Nối Tri Thức, tập trung vào việc rèn luyện kỹ năng giải bài toán về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.

Tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Cho hình chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b.

Đề bài

Cho hình chóp đều S.ABC, đáy có cạnh bằng a, cạnh bên bằng b.

a) Tính sin của góc tạo bởi cạnh bên và mặt đáy.

b) Tính tang của góc giữa mặt phẳng chứa mặt đáy và mặt phẳng chứa mặt bên.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Bài 7.19 trang 53 SGK Toán 11 tập 2 - Kết nối tri thức 1

- Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.

- Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt nằm trong mặt phẳng vuông góc vào giao tuyến hai mặt phẳng tại cùng 1 điểm.

Lời giải chi tiết

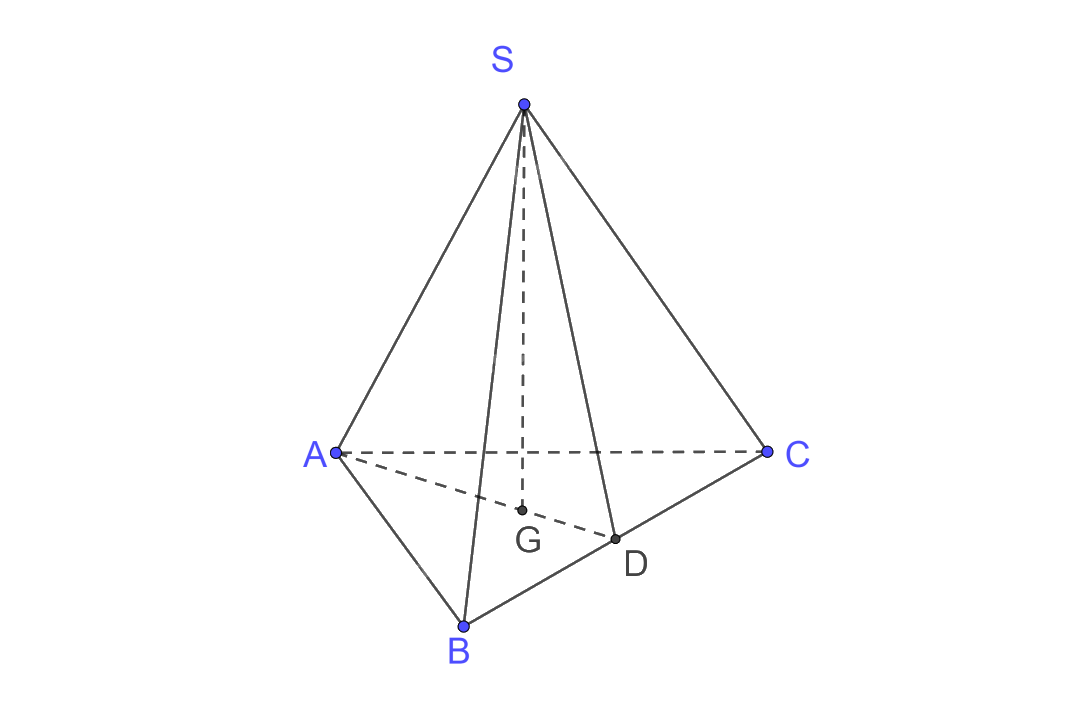
Bài 7.19 trang 53 SGK Toán 11 tập 2 - Kết nối tri thức 2

Vì hình chóp S.ABC đều, gọi G là hình chiếu của S trên (ABC) nên G là tâm của đáy ABC là tam giác đều do đó G cũng là trọng tâm hay trực tâm của tam giác ABC.

Gọi AG cắt BC tại D

a) Ta có A là hình chiếu của A trên (ABC)

G là hình chiếu của S trên (ABC)

\( \Rightarrow \) AG là hình chiếu của SA trên (ABC)

\( \Rightarrow \left( {SA,\left( {ABC} \right)} \right) = \left( {SA,AG} \right) = \widehat {SAG}\)

Tam giác ABC đều cạnh a nên \(AD = \frac{{a\sqrt 3 }}{2}\)

Mà G là trọng tâm nên \(AG = \frac{2}{3}AD = \frac{{a\sqrt 3 }}{3}\)

Xét tam giác SAG vuông tại G có

\(SG = \sqrt {S{A^2} - A{G^2}} = \sqrt {{b^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} \)

\(\sin \widehat {SAG} = \frac{{SG}}{{SA}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} :b = \sqrt {1 - \frac{{{a^2}}}{{3{b^2}}}} \)

b) Ta có \(AG \bot BC,SG \bot BC \Rightarrow BC \bot \left( {SAD} \right);SD \subset \left( {SAD} \right) \Rightarrow BC \bot SD\)

\(BC \bot AD\) (G là trực tâm)

\(\begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\ \Rightarrow \left( {\left( {SBC} \right),\left( {ABC} \right)} \right) = \left( {AD,SD} \right) = \widehat {SDA}\end{array}\)

Mà G là trọng tâm nên \(GD = \frac{1}{3}AD = \frac{{a\sqrt 3 }}{6}\)

Xét tam giác SGD vuông tại G có

\(\tan \widehat {SGD} = \frac{{SG}}{{GD}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} :\frac{{a\sqrt 3 }}{6} = \frac{6}{{a\sqrt 3 }}.\sqrt {{b^2} - \frac{{{a^2}}}{3}} \)

Bài 7.19 Trang 53 SGK Toán 11 Tập 2 - Kết Nối Tri Thức: Giải Chi Tiết và Hướng Dẫn

Bài 7.19 trang 53 SGK Toán 11 Tập 2 Kết Nối Tri Thức là một bài tập quan trọng trong chương trình học, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của nó. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:

Nội dung bài tập:

Bài tập yêu cầu chúng ta khảo sát hàm số và tìm các điểm cực trị, khoảng đồng biến, nghịch biến. Cụ thể, bài tập có thể yêu cầu:

Tính đạo hàm bậc nhất và bậc hai của hàm số.
Tìm các điểm cực trị của hàm số.
Xác định khoảng đồng biến và nghịch biến của hàm số.
Vẽ đồ thị hàm số.

Lời giải chi tiết:

Để giải bài tập này, chúng ta cần thực hiện các bước sau:

Bước 1: Tính đạo hàm bậc nhất (y') của hàm số. Sử dụng các quy tắc đạo hàm cơ bản để tính đạo hàm của hàm số.
Bước 2: Tìm các điểm cực trị. Giải phương trình y' = 0 để tìm các điểm nghiệm. Sau đó, xét dấu của y' để xác định các điểm cực đại, cực tiểu.
Bước 3: Tính đạo hàm bậc hai (y'') của hàm số. Sử dụng các quy tắc đạo hàm để tính đạo hàm bậc hai.
Bước 4: Xác định khoảng đồng biến và nghịch biến. Xét dấu của y' trên các khoảng xác định của hàm số. Nếu y' > 0 thì hàm số đồng biến, nếu y' < 0 thì hàm số nghịch biến.
Bước 5: Vẽ đồ thị hàm số. Dựa vào các thông tin đã tìm được, vẽ đồ thị hàm số.

Ví dụ minh họa:

Giả sử hàm số cần khảo sát là y = x³ - 3x² + 2.

Bước 1: y' = 3x² - 6x

Bước 2: Giải phương trình 3x² - 6x = 0, ta được x = 0 và x = 2. Xét dấu của y', ta thấy:

x < 0: y' > 0 (hàm số đồng biến)
0 < x < 2: y' < 0 (hàm số nghịch biến)
x > 2: y' > 0 (hàm số đồng biến)

Vậy hàm số có cực đại tại x = 0 và cực tiểu tại x = 2.

Bước 3: y'' = 6x - 6

Bước 4: Khoảng đồng biến: (-∞; 0) và (2; +∞). Khoảng nghịch biến: (0; 2).

Lưu ý quan trọng:

Khi giải bài tập về khảo sát hàm số, cần chú ý đến tập xác định của hàm số và các điểm không xác định. Ngoài ra, cần kiểm tra lại kết quả để đảm bảo tính chính xác.

Bài tập tương tự:

Để rèn luyện thêm kỹ năng giải bài tập về khảo sát hàm số, bạn có thể tham khảo các bài tập tương tự trong SGK Toán 11 Tập 2 Kết Nối Tri Thức hoặc trên các trang web học tập trực tuyến.

Tusach.vn - Nguồn tài liệu học tập Toán 11 uy tín:

Tusach.vn là một nguồn tài liệu học tập Toán 11 uy tín, cung cấp đầy đủ các bài giải, lời giải chi tiết và các bài tập tương tự. Hãy truy cập tusach.vn để học tập và ôn luyện hiệu quả!

Khái niệm	Giải thích
Đạo hàm	Tốc độ thay đổi tức thời của hàm số.
Điểm cực trị	Điểm mà tại đó hàm số đạt cực đại hoặc cực tiểu.
Khoảng đồng biến	Khoảng mà hàm số tăng.
Khoảng nghịch biến	Khoảng mà hàm số giảm.