Giải mục 2 trang 97, 98 SGK Toán 11 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 2 trang 97, 98 SGK Toán 11 tập 1 - Kết nối tri thức
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa Toán 11 tập 1 - Kết nối tri thức. Chúng tôi hiểu rằng việc tự học đôi khi gặp khó khăn, vì vậy chúng tôi luôn cố gắng mang đến những giải pháp tốt nhất để giúp bạn học tập hiệu quả.
Bài viết này sẽ tập trung vào việc giải mục 2 trang 97 và 98, giúp bạn hiểu rõ các khái niệm và phương pháp giải bài tập liên quan.
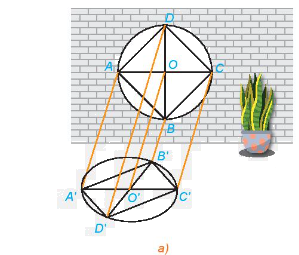
Quan sát Hình 4.56a và trả lời các câu hỏi sau: a) Hình chiếu O’ của điểm O có nằm trên đoạn A’C’ hay không? b) Hình chiếu của hai song cửa AB và CD như thế nào với nhau? c) Hình chiếu O’ của điểm O có phải là trung điểm của đoạn A’C’ hay
HĐ 2
Video hướng dẫn giải
Quan sát Hình 4.56a và trả lời các câu hỏi sau:
a) Hình chiếu O’ của điểm O có nằm trên đoạn A’C’ hay không?
b) Hình chiếu của hai song cửa AB và CD như thế nào với nhau?
c) Hình chiếu O’ của điểm O có phải là trung điểm của đoạn A’C’ hay không?
Phương pháp giải:
Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.Phép chiếu song song biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng.
Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.
Lời giải chi tiết:
a) Hình chiếu O’ của điểm O nằm trên đoạn A’C’.
b) Hình chiếu song song của AB và CD song song với AB và CD.
c) Hình chiếu O’ của điểm O là trung điểm của đoạn A’C’.
LT 2
Video hướng dẫn giải
Chứng minh rằng hình chiếu song song của một hình thang là một hình thang (H.4.61).

Phương pháp giải:
Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.Phép chiếu song song biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng.
Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.
Lời giải chi tiết:
Vì ABCD là hình thang nên AB // CD, do đó hình chiếu của AB là A'B' song song với hình chiếu của CD là C'D'.
Tứ giác A'B'C'D' có A'B' // C'D' nên nó là hình thang.
LT 3
Video hướng dẫn giải
Một phép chiếu song song biến tam giác ABC thành tam giác A’B’C’, biến M thành M’. Chứng minh rằng phép chiếu đó biến đường trung bình của tam giác ABC thành đường trung bình của tam giác A’B’C’.

Phương pháp giải:
Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.
Phép chiếu song song biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng.
Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.
Lời giải chi tiết:
Gọi N là trung điểm của AC. Khi đó MN là đường trung bình của tam giác ABC.
Vì M là trung điểm của BC nên B, M, C thẳng hàng theo thứ tự đó và \(\frac{{BM}}{{MC}} = 1\).
Do vậy, B’, M’, C’ thẳng hàng theo thứ tự đó và \(\frac{{B'M'}}{{M'C'}} = 1\).
Tức M’ là trung điểm của B’C’.
Tương tự, N’ là trung điểm của A’C’.
Vậy M’N’ là đường trung bình của tam giác A’B’C’.
Giải mục 2 trang 97, 98 SGK Toán 11 tập 1 - Kết nối tri thức: Hướng dẫn chi tiết và dễ hiểu
Mục 2 của chương trình Toán 11 tập 1 - Kết nối tri thức thường xoay quanh các chủ đề về hàm số lượng giác, bao gồm các khái niệm như tập xác định, tập giá trị, tính đơn điệu, cực trị và ứng dụng của hàm số lượng giác trong giải quyết các bài toán thực tế. Việc nắm vững kiến thức này là nền tảng quan trọng để học tốt các chương tiếp theo.
Nội dung chính của Mục 2 trang 97, 98
Thông thường, mục 2 trang 97, 98 sẽ bao gồm các bài tập sau:
- Bài 1: Xác định tập xác định của hàm số lượng giác.
- Bài 2: Tìm tập giá trị của hàm số lượng giác.
- Bài 3: Xét tính đơn điệu của hàm số lượng giác trên một khoảng cho trước.
- Bài 4: Tìm cực trị của hàm số lượng giác.
- Bài 5: Ứng dụng hàm số lượng giác để giải các bài toán về hình học hoặc vật lý.
Hướng dẫn giải chi tiết các bài tập
Để giải các bài tập này một cách hiệu quả, bạn cần nắm vững các công thức lượng giác cơ bản, các phương pháp xét dấu và sử dụng đạo hàm (nếu cần). Dưới đây là hướng dẫn chi tiết cho từng bài tập:
Bài 1: Xác định tập xác định của hàm số lượng giác
Tập xác định của hàm số lượng giác là tập hợp tất cả các giá trị của x sao cho biểu thức trong hàm số có nghĩa. Ví dụ, với hàm số y = tan(x), tập xác định là tất cả các giá trị của x sao cho x ≠ π/2 + kπ (k là số nguyên).
Bài 2: Tìm tập giá trị của hàm số lượng giác
Tập giá trị của hàm số lượng giác là tập hợp tất cả các giá trị mà y có thể nhận được. Ví dụ, với hàm số y = sin(x), tập giá trị là [-1, 1].
Bài 3: Xét tính đơn điệu của hàm số lượng giác
Để xét tính đơn điệu của hàm số lượng giác, bạn có thể sử dụng đạo hàm hoặc dựa vào đồ thị của hàm số. Ví dụ, hàm số y = cos(x) nghịch biến trên khoảng (0, π).
Bài 4: Tìm cực trị của hàm số lượng giác
Để tìm cực trị của hàm số lượng giác, bạn cần tìm các điểm mà đạo hàm bằng 0 hoặc không tồn tại. Sau đó, xét dấu của đạo hàm để xác định xem đó là điểm cực đại hay cực tiểu.
Bài 5: Ứng dụng hàm số lượng giác
Các bài tập ứng dụng hàm số lượng giác thường yêu cầu bạn sử dụng kiến thức về hàm số lượng giác để giải quyết các bài toán về hình học hoặc vật lý. Ví dụ, bạn có thể sử dụng hàm số lượng giác để tính chiều cao của một tòa nhà hoặc khoảng cách giữa hai điểm.
Lưu ý khi giải bài tập
Khi giải bài tập về hàm số lượng giác, bạn cần lưu ý những điều sau:
- Nắm vững các công thức lượng giác cơ bản.
- Sử dụng đạo hàm một cách hợp lý.
- Kiểm tra lại kết quả sau khi giải xong.
- Tham khảo các tài liệu và nguồn học tập khác để hiểu rõ hơn về kiến thức.
Tusach.vn – Đồng hành cùng bạn trên con đường học tập
Tusach.vn luôn cập nhật và cung cấp lời giải chi tiết, chính xác cho tất cả các bài tập trong SGK Toán 11 tập 1 - Kết nối tri thức. Hãy truy cập website của chúng tôi để được hỗ trợ tốt nhất trong quá trình học tập của bạn. Chúc bạn học tập tốt!
| Hàm số | Tập xác định | Tập giá trị |
|---|---|---|
| y = sin(x) | R | [-1, 1] |
| y = cos(x) | R | [-1, 1] |
| y = tan(x) | x ≠ π/2 + kπ | R |