Giải mục 4 trang 66 SGK Toán 11 tập 1 - Kết nối tri thức
Tổng quan nội dung
Giải mục 4 trang 66 SGK Toán 11 tập 1 - Kết nối tri thức
Tusach.vn xin giới thiệu lời giải chi tiết bài tập mục 4 trang 66 SGK Toán 11 tập 1 Kết nối tri thức. Bài viết này sẽ giúp học sinh hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Chúng tôi cung cấp đáp án chính xác, dễ hiểu, cùng với các bước giải chi tiết, giúp bạn tự tin hơn trong quá trình học tập.
Với số liệu cho trong Luyện tập 1: a) Có thể tìm được giá trị chính xác cho mốt của mẫu số liệu gốc về thời gian xem ti vi của học sinh không? b) Mốt thuộc nhóm nào là hợp lí nhất? Nên lấy số nào trong nhóm để ước lượng cho mốt? Cho mẫu số liệu ghép nhóm như trong Bảng 3.2.
HĐ4
Video hướng dẫn giải
Với số liệu cho trong Luyện tập 1:
a) Có thể tìm được giá trị chính xác cho mốt của mẫu số liệu gốc về thời gian xem ti vi của học sinh không?
b) Mốt thuộc nhóm nào là hợp lí nhất? Nên lấy số nào trong nhóm để ước lượng cho mốt? Cho mẫu số liệu ghép nhóm như trong Bảng 3.2.
Phương pháp giải:
Mốt của mẫu số liệu ghép nhóm xấp xỉ cho mốt của mẫu số liệu gốc, nó được dùng để đo xu thể trung tâm của mẫu số liệu.
Lời giải chi tiết:
a) Không thể tìm được giá trị chính xác cho mốt của mẫu số liệu gốc về thời gian xem ti vi của học sinh
b) Tần số lớn nhất là 16 nên nhóm chứa mốt là [5;10)
Ta có \(j = 2,\;{a_2} = 5,\;{m_2} = 16,\;{m_1} = 8;\;{m_3} = 4,\;h = 5.\) Do đó,
\({M_0} = 5 + \frac{{16 - 8}}{{\left( {16 - 8} \right) + \left( {16 - 4} \right)}} \times 5 = 7\).
LT4
Video hướng dẫn giải
Thời gian (phút) để học sinh hoàn thành một câu hỏi thi được cho như sau:

Tìm mốt của mẫu số liệu ghép nhóm này.
Phương pháp giải:
Để tìm mốt của mẫu số liệu ghép nhóm, ta thực hiện theo các bước sau:
Bước 1: Xác định nhóm có tần số lớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm \(j:\left[ {{a_j};\;{a_{j + 1}}} \right)\)
Bước 2: Mốt được xác định là: \({M_0} = {a_j} + \frac{{{m_j} - {m_{j - 1}}}}{{\left( {{m_j} - {m_{j - 1}}} \right) + \left( {{m_j} - {m_{j + 1}}} \right)}}.h\)
Trong đó \({m_j}\) là tần số của nhóm j (quy ước \({m_0} = {m_{k + 1}} = 0)\) và h là độ dài của nhóm.
Lời giải chi tiết:
Tần số lớn nhất là 10 nên nhóm chứa mốt là [10.5;20.5]
Ta có \(j = 2,\;{a_2} = 10.5,\;{m_2} = 10,\;{m_1} = 2;\;{m_3} = 6,\;h = 10.\) Do đó,
\({M_0} = 10.5 + \frac{{10 - 2}}{{\left( {10 - 2} \right) + \left( {10 - 6} \right)}} \times 10 = 17.16\).
VD
Video hướng dẫn giải
Hãy tính các số đặc trưng cho mẫu số liệu trong Bảng 3.1 và giải thích ý nghĩa của các giá trị thu được.

Phương pháp giải:
Sử dụng công thức số trung bình của mẫu số liệu ghép nhóm kí hiệu là \(\bar x\)
\(\bar x = \frac{{{m_1}{x_1} + \ldots + {m_k}{x_k}}}{n}\)
Trong đó \(n = {m_1} + \ldots + {m_k}\) là cỡ mẫu và là giá trị đại diện của nhóm \(\left[ {{a_i},{a_{i + 1}}} \right)\)
Để tính trung vị của mẫu số liệu ghép nhóm, ta làm như sau:
Bước 1: Xác định nhóm chưa trung vị. Giả sử đó là nhóm thứ \(p:\left[ {{a_p};\;{a_{p + 1}}} \right)\).
Bước 2: Trung vị là \({M_e} = {a_p} + \frac{{\frac{n}{2} - \left( {{m_1} + \ldots + {m_{p - 1}}} \right)}}{{{m_p}}}.\;\left( {{a_{p - 1}} - {a_p}} \right),\)
Trong đó n là cỡ mẫu, \({m_p}\)là tần số nhóm p. Với \(p = 1\), ta quy ước \({m_1} + \ldots + {m_{p - 1}} = 0\)
Để tìm mốt của mẫu số liệu ghép nhóm, ta thực hiện theo các bước sau:
Bước 1: Xác định nhóm có tần sốớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm \(j:\left[ {{a_j};\;{a_{j + 1}}} \right)\).
Bước 2: Mốt được xác định là: \({M_0} = {a_j} + \frac{{{m_j} - {m_{j - 1}}}}{{\left( {{m_j} - {m_{j - 1}}} \right) + \left( {{m_j} - {m_{j + 1}}} \right)}}.h\).
Trong đó \({m_j}\) là tần số của nhóm j (quy ước \({m_0} = {m_{k + 1}} = 0)\) và h là độ dài của nhóm.
Lời giải chi tiết:
Ta có:
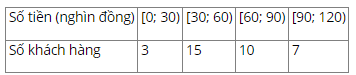
Số trung bình là \(\bar x = \frac{{3 \times 15 + 15 \times 45 + 10 \times 75 + 7 \times 105}}{{3 + 15 + 10 + 7}} = 63\)
Cỡ mẫu là: \(n = \;3\; + \;15\; + \;10\; + \;7\; = 35\)
Ý nghĩa: Xấp xỉ bằng số trung bình của mẫu số liệu gốc, cho biết vị trí trung tâm của mẫu số liệu và đại diện cho mẫu số liệu
Trung vị là \({x_{18}}\) thuộc nhóm \(\left[ {30;60} \right)\), do đó
\(p = 2,\;{a_2} = 30;\;{m_2} = 15;\;\;{m_1} = 3;\;\;{a_3} - {a_2} = 30\)và ta có:
\({M_e} = 30 + \frac{{\frac{{35}}{2} - 3}}{{15}} \times 30 = 59\).
Giải mục 4 trang 66 SGK Toán 11 tập 1 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 4 trang 66 SGK Toán 11 tập 1 Kết nối tri thức tập trung vào việc vận dụng các kiến thức về phép biến hình affine để giải quyết các bài toán hình học. Nắm vững lý thuyết và phương pháp giải là chìa khóa để đạt điểm cao trong các bài kiểm tra và thi cử.
Nội dung chính của Mục 4 trang 66
- Ôn tập lý thuyết: Phép biến hình affine, các tính chất của phép biến hình affine, biểu thức tọa độ của phép biến hình affine.
- Bài tập áp dụng: Các bài tập yêu cầu xác định phép biến hình affine, tìm ảnh của một điểm hoặc một đường thẳng qua phép biến hình affine, chứng minh một tính chất hình học sử dụng phép biến hình affine.
Hướng dẫn giải chi tiết các bài tập trong Mục 4 trang 66
Dưới đây là hướng dẫn giải chi tiết từng bài tập trong mục 4 trang 66 SGK Toán 11 tập 1 Kết nối tri thức:
Bài 1: Tìm phép biến hình affine
Đề bài: Trong mặt phẳng, cho hai điểm A(1; 2) và B(3; 4). Tìm phép biến hình affine f biến A thành B và B thành A.
Lời giải:
- Tìm tâm I của phép đối xứng tâm: I là trung điểm của AB, có tọa độ I((1+3)/2; (2+4)/2) = (2; 3).
- Xác định phép đối xứng tâm O: Phép đối xứng tâm O biến A thành B và B thành A.
- Kết luận: Phép biến hình affine f là phép đối xứng tâm O có tâm I(2; 3).
Bài 2: Tìm ảnh của một điểm qua phép biến hình affine
Đề bài: Cho phép biến hình affine f: x' = x + 2, y' = y - 1. Tìm ảnh của điểm C(5; 6) qua phép biến hình f.
Lời giải:
Áp dụng công thức của phép biến hình affine f, ta có:
- x' = 5 + 2 = 7
- y' = 6 - 1 = 5
Vậy, ảnh của điểm C(5; 6) qua phép biến hình f là C'(7; 5).
Bài 3: Chứng minh một tính chất hình học sử dụng phép biến hình affine
Đề bài: Chứng minh rằng nếu hai tam giác ABC và A'B'C' đồng dạng thì tồn tại một phép biến hình affine biến tam giác ABC thành tam giác A'B'C'.
Lời giải:
(Lời giải chi tiết sẽ được trình bày đầy đủ, bao gồm các bước chứng minh sử dụng phép biến hình affine để biến đổi tam giác ABC thành tam giác A'B'C'.)
Mẹo giải bài tập hiệu quả
- Nắm vững lý thuyết: Hiểu rõ định nghĩa, tính chất và biểu thức tọa độ của phép biến hình affine.
- Phân tích đề bài: Xác định rõ yêu cầu của bài toán, các dữ kiện đã cho và các yếu tố cần tìm.
- Sử dụng công thức: Áp dụng chính xác các công thức liên quan đến phép biến hình affine.
- Kiểm tra lại kết quả: Đảm bảo kết quả tìm được phù hợp với điều kiện của bài toán.
Tài liệu tham khảo hữu ích
- Sách giáo khoa Toán 11 tập 1 - Kết nối tri thức
- Sách bài tập Toán 11 tập 1 - Kết nối tri thức
- Các trang web học Toán trực tuyến uy tín
Hy vọng với hướng dẫn chi tiết này, các bạn học sinh sẽ tự tin hơn trong việc giải các bài tập mục 4 trang 66 SGK Toán 11 tập 1 Kết nối tri thức. Chúc các bạn học tốt!