Lý thuyết Phép chiếu vuông góc, góc giữa đường thẳng và mặt phẳng - Toán 11 Kết nối tri thức
Tổng quan nội dung
Lý thuyết Phép chiếu vuông góc, góc giữa đường thẳng và mặt phẳng
Chương trình Toán 11 Kết nối tri thức, chủ đề về Phép chiếu vuông góc và góc giữa đường thẳng và mặt phẳng là một phần quan trọng của hình học không gian. Nắm vững kiến thức này là nền tảng để giải quyết các bài toán phức tạp hơn.
Bài viết này của tusach.vn sẽ cung cấp lý thuyết chi tiết, các định nghĩa, tính chất quan trọng và ví dụ minh họa giúp bạn hiểu rõ về chủ đề này.
1. Phép chiếu vuông góc
1. Phép chiếu vuông góc
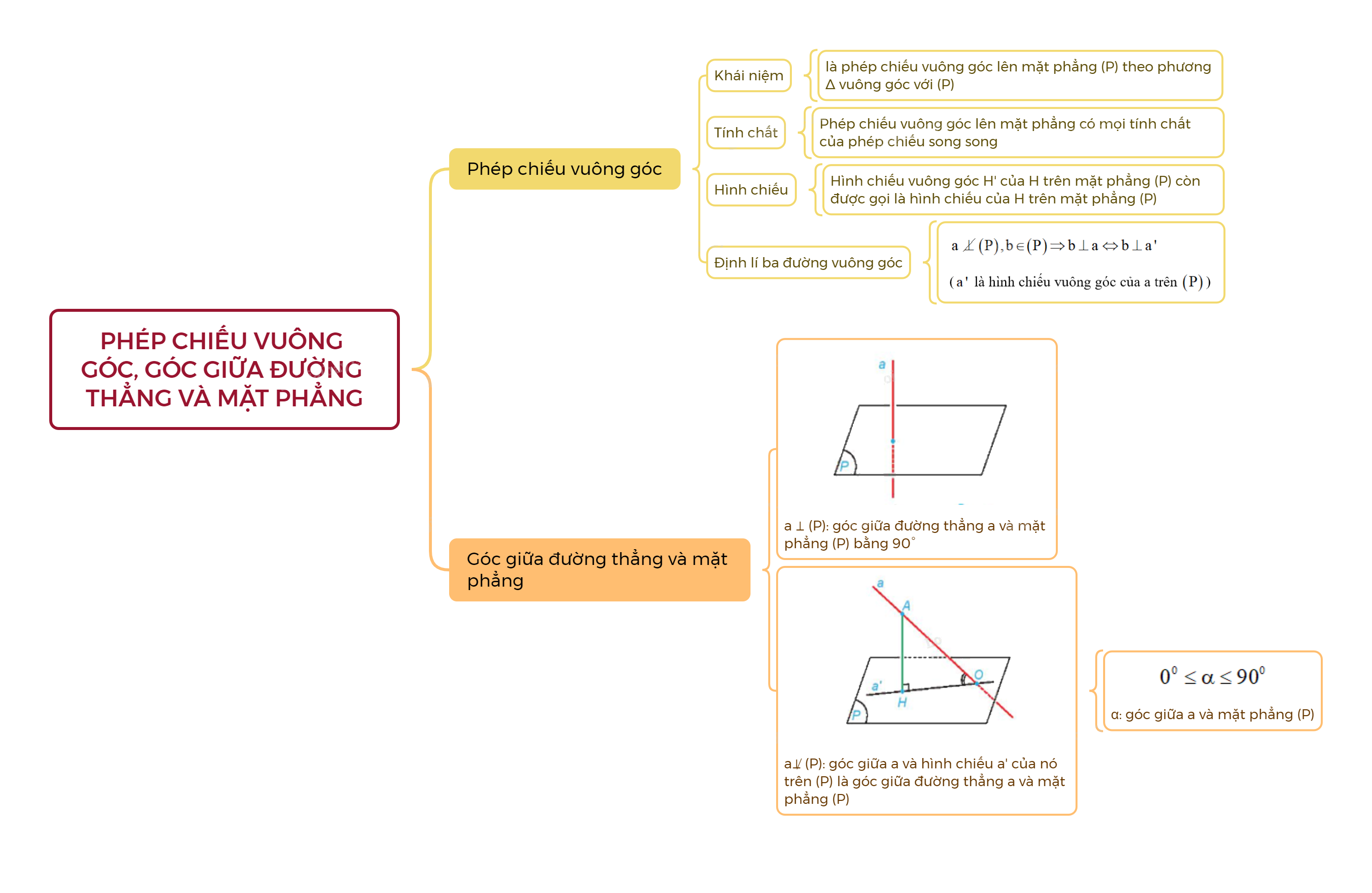
Phép chiếu vuông góc lên mặt phẳng (P) theo phương \(\Delta \) vuông góc với (P) được gọi là phép chiều vuông góc lên mặt phẳng (P).
Chú ý:
- Vì phép chiếu vuông góc lên một mặt phẳng là một trường hợp đặc biệt của phép chiếu song song nên nó có mọi tính chất của phép chiếu song song.
- Phép chiếu vuông góc lên mặt phẳng (P) còn được gọi đơn giản là phép chiếu lên mặt phẳng (P). Hình chiếu vuông góc H’của hình H trên mặt phẳng (P) còn được gọi là hình chiếu của H trên mặt phẳng (P).
Định lí ba đường vuông góc:
Cho đường thẳng a và mặt phẳng (P) không vuông góc với nhau. Khi đó, một đường thẳng b nằm trong mặt phẳng (P) vuông góc với đường thẳng a khi và chỉ khi b vuông góc với hình chiếu vuông góc a’ của a trên (P).
2. Góc giữa đường thẳng và mặt phẳng
Nếu đường thẳng a vuông góc với mặt phẳng (P) thì ta nói rằng góc giữa đường thẳng a và mặt phẳng (P) bằng \({90^0}\).
Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa a và hình chiếu a’ của nó trên (P) được gọi là góc giữa đường thẳng a và mặt phẳng (P).
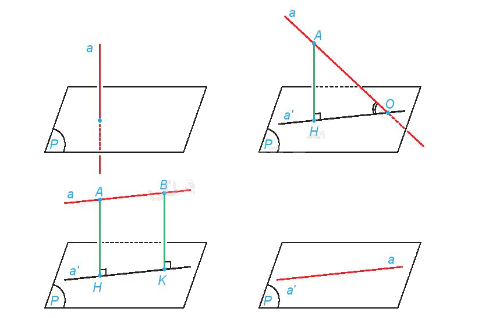
Chú ý: Nếu \(\alpha \) là góc giữa đường thẳng a và mặt phẳng (P) thì \({0^0} \le \alpha \le {90^0}\).
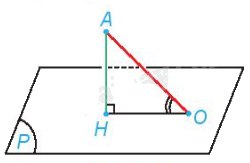
Nhận xét: Nếu điểm A có hình chiếu H trên mặt phẳng (P). Lấy điểm O thuộc mặt phẳng (P), O không trung H. Khi đó góc giữa đường thẳng AO và mặt phẳng (P) bằng góc AOH.
Lý Thuyết Phép Chiếu Vuông Góc, Góc Giữa Đường Thẳng và Mặt Phẳng - Toán 11 Kết Nối Tri Thức
Chương trình Toán 11 Kết nối tri thức đi sâu vào hình học không gian, và một trong những chủ đề cốt lõi là phép chiếu vuông góc và góc giữa đường thẳng và mặt phẳng. Việc nắm vững lý thuyết này không chỉ giúp học sinh giải quyết các bài tập trong sách giáo khoa mà còn là nền tảng cho các kiến thức toán học nâng cao hơn.
1. Phép Chiếu Vuông Góc
Định nghĩa: Phép chiếu vuông góc của điểm M lên mặt phẳng (P) là điểm H sao cho MH vuông góc với (P). H được gọi là hình chiếu vuông góc của M lên (P).
Định lý: Nếu đường thẳng d vuông góc với mặt phẳng (P) thì mọi điểm thuộc d đều là hình chiếu vuông góc của chính nó lên (P).
Cách xác định hình chiếu vuông góc:
- Nếu M thuộc (P) thì hình chiếu của M chính là M.
- Nếu M không thuộc (P), ta tìm đường thẳng d vuông góc với (P) tại M. Giao điểm của d và (P) là hình chiếu vuông góc của M lên (P).
2. Góc Giữa Đường Thẳng và Mặt Phẳng
Định nghĩa: Góc giữa đường thẳng d và mặt phẳng (P) là góc giữa đường thẳng d và hình chiếu của d trên mặt phẳng (P).
Cách tính góc:
- Tìm hình chiếu d' của d trên (P).
- Tính góc θ giữa d và d' (θ là góc nhọn).
Công thức: Nếu d vuông góc với (P) thì góc giữa d và (P) bằng 90°.
3. Góc Giữa Hai Đường Thẳng
Định nghĩa: Góc giữa hai đường thẳng d1 và d2 là góc nhọn tạo bởi hai đường thẳng đó.
Cách tính góc:
- Nếu d1 và d2 song song thì góc giữa chúng bằng 0°.
- Nếu d1 và d2 cắt nhau, ta tìm vector chỉ phương của hai đường thẳng và sử dụng công thức tính góc giữa hai vector.
4. Bài Tập Minh Họa
Bài tập 1: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy. Tính góc giữa đường thẳng SA và mặt phẳng (ABCD).
Giải: Vì SA vuông góc với (ABCD) nên góc giữa SA và (ABCD) bằng 90°.
Bài tập 2: Cho hai đường thẳng d1 và d2 cắt nhau tại A. Tìm góc giữa d1 và d2 biết vector chỉ phương của d1 là u1 = (1, 0, 0) và vector chỉ phương của d2 là u2 = (1, 1, 0).
Giải: Sử dụng công thức tính góc giữa hai vector: cos θ = (u1 . u2) / (||u1|| . ||u2||) = (1*1 + 0*1 + 0*0) / (1*√2) = 1/√2. Vậy θ = 45°.
5. Lưu Ý Quan Trọng
Khi giải các bài toán liên quan đến phép chiếu vuông góc và góc giữa đường thẳng và mặt phẳng, cần chú ý:
- Xác định đúng hình chiếu vuông góc.
- Sử dụng các định lý và công thức một cách chính xác.
- Vẽ hình minh họa để dễ dàng hình dung và giải quyết bài toán.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và hữu ích về lý thuyết Phép chiếu vuông góc, góc giữa đường thẳng và mặt phẳng - Toán 11 Kết nối tri thức. Hãy luyện tập thêm nhiều bài tập để nắm vững kiến thức và tự tin giải quyết các bài toán khó hơn.