Bài 4.32 Trang 100 SGK Toán 11 Tập 1 - Kết Nối Tri Thức

Bài 4.32 trang 100 SGK Toán 11 tập 1 - Kết nối tri thức

Bài 4.32 trang 100 SGK Toán 11 Tập 1 - Kết Nối Tri Thức

Bài 4.32 thuộc chương trình Toán 11 Tập 1, sách Kết Nối Tri Thức, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến vectơ. Bài tập này yêu cầu học sinh vận dụng kiến thức về tích vô hướng của hai vectơ để giải quyết các vấn đề thực tế.

tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.

Hình 4.65 có thể là hình biểu diễn của một hình lục giác đều hay không? Vì sao?

Đề bài

Hình 4.65 có thể là hình biểu diễn của một hình lục giác đều hay không? Vì sao?

Bài 4.32 trang 100 SGK Toán 11 tập 1 - Kết nối tri thức 1

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết Bài 4.32 trang 100 SGK Toán 11 tập 1 - Kết nối tri thức 2

Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó.Phép chiếu song song biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thăng.

Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.

Lời giải chi tiết

Xét hình lục giác đều MNPQRS có tâm O.

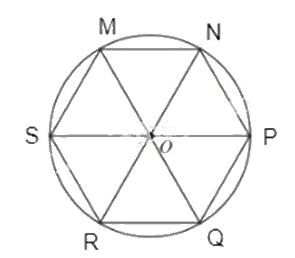
Ta thấy:

- Tứ giác OSMN là hình thoi;

- Các điểm P, Q, R lần lượt là các điểm đối xứng của các điểm S, M, N qua tâm O.

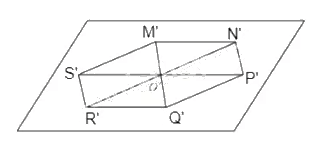
Từ đó suy ra cách vẽ hình biểu diễn của hình lục giác đều MNPQRS như sau:

- Vẽ hình bình hành O’S’M’N’ biểu diễn cho hình thoi OSMN;

- Lấy các điểm P’, Q’, R’ lần lượt là các điểm đối xứng của các điểm S’, M’, N’ qua O’, ta được hình biểu diễn của M’N’P’Q’R’S’ của hình lục giác đều MNPQRS.

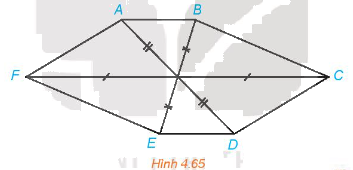
+ Gọi I là giao điểm các đường chéo AD, BE và CF trong hình lục giác ABCDEF

Bài 4.32 trang 100 SGK Toán 11 tập 1 - Kết nối tri thức 4

Khi đó nếu ABCDEF là hình biểu diễn của hình lục giác đều thì phải thỏa mãn hai điều kiện:

- Tứ giác IFAB là hình bình hành (1)

- D, E, F lần lượt là các điểm đối xứng của các điểm A, B, C qua I (2)

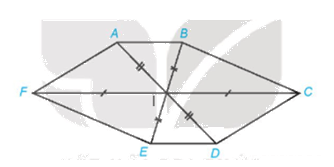
Bài 4.32 trang 100 SGK Toán 11 tập 1 - Kết nối tri thức 5

Từ hình vẽ ta thấy điều kiện (2) thỏa mãn nhưng điều kiện (1) không thỏa mãn. Vậy hình 4.65 không thể là hình biểu diễn của một hình lục giác đều.

Bài 4.32 Trang 100 SGK Toán 11 Tập 1 - Kết Nối Tri Thức: Giải Chi Tiết và Hướng Dẫn

Bài 4.32 trang 100 SGK Toán 11 Tập 1 Kết Nối Tri Thức là một bài tập quan trọng giúp học sinh củng cố kiến thức về tích vô hướng của hai vectơ và ứng dụng của nó trong hình học. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:

Nội dung bài tập:

Bài 4.32 yêu cầu học sinh sử dụng kiến thức về tích vô hướng để chứng minh một số tính chất hình học hoặc giải quyết các bài toán liên quan đến góc giữa hai vectơ. Thông thường, bài tập sẽ cho trước một số vectơ và yêu cầu tính góc giữa chúng, hoặc chứng minh một đẳng thức liên quan đến tích vô hướng.

Lời giải chi tiết:

Để giải bài 4.32, học sinh cần nắm vững các công thức và tính chất sau:

Tích vô hướng của hai vectơ:a ⋅ b = |a| |b| cos(θ), trong đó θ là góc giữa hai vectơ a và b.
Công thức tính cosin góc giữa hai vectơ:cos(θ) = (a ⋅ b) / (|a| |b|)
Các tính chất của tích vô hướng:a ⋅ b = b ⋅ a, a ⋅ (b + c) = a ⋅ b + a ⋅ c, a ⋅ a = |a|^2

Ví dụ minh họa (giả định bài tập cụ thể):

Giả sử bài tập yêu cầu chứng minh rằng tam giác ABC vuông tại A, biết AB = (1; 2), AC = (3; -1), BC = (2; -3).

Tính tích vô hướng của AB và AC:AB ⋅ AC = (1 * 3) + (2 * -1) = 1
Nếu AB ⋅ AC = 0 thì AB vuông góc với AC, suy ra tam giác ABC vuông tại A. Trong trường hợp này, tích vô hướng không bằng 0, do đó cần kiểm tra bằng cách sử dụng định lý Pytago.
Tính độ dài các cạnh:
- |AB| = √(1^2 + 2^2) = √5
- |AC| = √(3^2 + (-1)^2) = √10
- |BC| = √(2^2 + (-3)^2) = √13
Kiểm tra định lý Pytago:|AB|^2 + |AC|^2 = 5 + 10 = 15 ≠ 13 = |BC|^2. Do đó, tam giác ABC không vuông tại A.

Mẹo giải nhanh:

Khi gặp bài tập liên quan đến tích vô hướng, hãy luôn nhớ đến công thức tính cosin góc giữa hai vectơ. Nếu góc giữa hai vectơ bằng 90 độ, thì tích vô hướng của chúng bằng 0.

Bài tập tương tự:

Để rèn luyện thêm kỹ năng giải bài tập về tích vô hướng, bạn có thể tham khảo các bài tập sau:

Bài 4.33 trang 100 SGK Toán 11 Tập 1 Kết Nối Tri Thức
Bài 4.34 trang 101 SGK Toán 11 Tập 1 Kết Nối Tri Thức

Kết luận:

Bài 4.32 trang 100 SGK Toán 11 Tập 1 Kết Nối Tri Thức là một bài tập quan trọng giúp học sinh hiểu sâu hơn về tích vô hướng của hai vectơ và ứng dụng của nó trong hình học. Bằng cách nắm vững các công thức và tính chất liên quan, học sinh có thể tự tin giải quyết các bài tập tương tự.

Chúc các bạn học tốt!