Lý Thuyết Các Quy Tắc Tính Đạo Hàm - Toán 11 Kết Nối Tri Thức

Lý thuyết Các quy tắc tính đạo hàm - Toán 11 Kết nối tri thức

Lý thuyết Các Quy Tắc Tính Đạo Hàm - Toán 11 Kết Nối Tri Thức

Chào mừng bạn đến với bài tổng hợp lý thuyết các quy tắc tính đạo hàm dành cho học sinh lớp 11 chương trình Kết Nối Tri Thức. Bài viết này sẽ cung cấp một cách hệ thống và dễ hiểu các kiến thức cơ bản về đạo hàm, các quy tắc tính đạo hàm thường gặp và cách áp dụng chúng vào giải bài tập.

Nắm vững lý thuyết là nền tảng quan trọng để giải quyết các bài toán liên quan đến đạo hàm một cách chính xác và hiệu quả. Hãy cùng tusach.vn khám phá ngay!

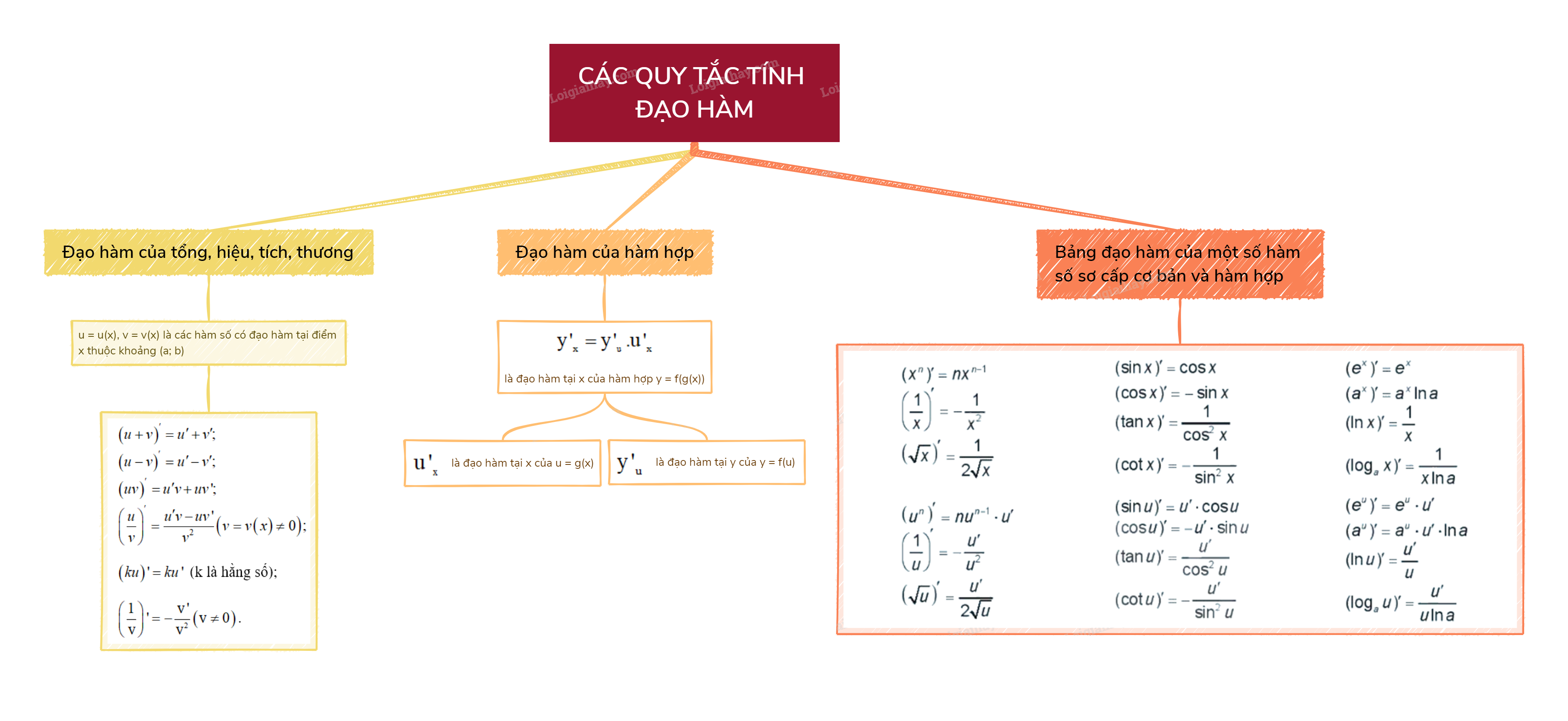
1. Đạo hàm của tổng, hiệu, tích, thương

1. Đạo hàm của tổng, hiệu, tích, thương

Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng (a; b). Khi đó

\(\begin{array}{*{20}{l}}{{{\left( {u + v} \right)}^\prime } = u' + v';}\\{{{\left( {u - v} \right)}^\prime } = u' - v';}\\{{{\left( {uv} \right)}^\prime } = u'v + uv';}\\{{{\left( {\frac{u}{v}} \right)}^\prime } = \frac{{u'v - uv'}}{{{v^2}}}\left( {v = v\left( x \right) \ne 0} \right);}\end{array}\)

\(\left( {ku} \right)' = ku'\) (k là hằng số);

\(\left( {\frac{1}{v}} \right)' = - \frac{{v'}}{{{v^2}}}\left( {v \ne 0} \right)\).

2. Đạo hàm của hàm hợp

Nếu hàm số u = g(x) có đạo hàm tại x là \(u{'_x}\) và hàm số y = f(u) có đạo hàm tại u là \(y{'_u}\) thì hàm hợp y = f(g(x)) có đạo hàm tại x là \(y{'_x} = y{'_u}.u{'_x}\).

3. Bảng đạo hàm của một số hàm số sơ cấp cơ bản và hàm hợp

Lý thuyết Các quy tắc tính đạo hàm - Toán 11 Kết nối tri thức 1

Lý thuyết Các quy tắc tính đạo hàm - Toán 11 Kết nối tri thức 2

Lý Thuyết Các Quy Tắc Tính Đạo Hàm - Toán 11 Kết Nối Tri Thức: Tổng Quan

Đạo hàm là một khái niệm nền tảng trong giải tích, mô tả tốc độ thay đổi tức thời của một hàm số. Trong chương trình Toán 11 Kết Nối Tri Thức, học sinh sẽ được làm quen với các quy tắc tính đạo hàm cơ bản, giúp đơn giản hóa việc tìm đạo hàm của các hàm số phức tạp.

1. Khái Niệm Đạo Hàm

Đạo hàm của hàm số f(x) tại điểm x₀, ký hiệu là f'(x₀), là giới hạn của tỷ số giữa độ biến thiên của hàm số và độ biến thiên của đối số khi độ biến thiên của đối số tiến tới 0 (nếu giới hạn này tồn tại).

Công thức: f'(x₀) = lim_Δx→0 [f(x₀ + Δx) - f(x₀)] / Δx

2. Các Quy Tắc Tính Đạo Hàm Cơ Bản

Quy tắc đạo hàm của hàm số lũy thừa: Nếu f(x) = xⁿ (n là số nguyên), thì f'(x) = nx^n-1
Quy tắc đạo hàm của hàm số đa thức: Đạo hàm của một đa thức là tổng các đạo hàm của từng hạng tử.
Quy tắc đạo hàm của tổng và hiệu: (u + v)' = u' + v'; (u - v)' = u' - v'
Quy tắc đạo hàm của tích: (uv)' = u'v + uv'
Quy tắc đạo hàm của thương: (u/v)' = (u'v - uv') / v²
Quy tắc đạo hàm của hàm hợp: Nếu y = f(u) và u = g(x), thì dy/dx = (dy/du) * (du/dx)

3. Đạo Hàm của Một Số Hàm Số Đặc Biệt

Hàm số f(x)	Đạo hàm f'(x)
sin(x)	cos(x)
cos(x)	-sin(x)
tan(x)	1/cos²(x)
e^x	e^x
ln(x)	1/x

4. Ví Dụ Minh Họa

Ví dụ 1: Tính đạo hàm của hàm số f(x) = 3x² + 2x - 1

Giải:

f'(x) = 3 * 2x¹ + 2 * 1 - 0 = 6x + 2

Ví dụ 2: Tính đạo hàm của hàm số f(x) = sin(2x)

Giải:

Đặt u = 2x, suy ra du/dx = 2. f(x) = sin(u), suy ra df/du = cos(u). Áp dụng quy tắc đạo hàm hàm hợp: f'(x) = (df/du) * (du/dx) = cos(u) * 2 = 2cos(2x)

5. Luyện Tập và Bài Tập

Để nắm vững lý thuyết và rèn luyện kỹ năng tính đạo hàm, bạn nên thực hành giải nhiều bài tập khác nhau. tusach.vn cung cấp một kho bài tập đa dạng với các mức độ khó khác nhau, giúp bạn tự tin hơn trong các kỳ thi.

Tính đạo hàm của các hàm số sau: f(x) = x³ - 5x + 2, f(x) = cos(x) + e^x
Tìm đạo hàm của hàm số f(x) = (x² + 1) / (x - 1)
Cho hàm số f(x) = sin(x²). Tính f'(x).

6. Kết Luận

Lý thuyết các quy tắc tính đạo hàm là một phần quan trọng trong chương trình Toán 11 Kết Nối Tri Thức. Việc nắm vững các quy tắc này sẽ giúp bạn giải quyết các bài toán liên quan đến đạo hàm một cách nhanh chóng và chính xác. Hãy luyện tập thường xuyên và đừng ngần ngại tìm kiếm sự giúp đỡ khi gặp khó khăn. Chúc bạn học tốt!