Giải mục 2 trang 55, 56, 57 SGK Toán 11 tập 2 - Kết nối tri thức
Tổng quan nội dung
Giải mục 2 trang 55, 56, 57 SGK Toán 11 tập 2 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 55, 56, 57 sách giáo khoa Toán 11 tập 2 chương trình Kết nối tri thức. Bài viết này sẽ giúp các em hiểu rõ hơn về các khái niệm và phương pháp giải bài tập trong chương trình học.
tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp những tài liệu và lời giải chính xác, dễ hiểu nhất.
Cho đường thẳng a song song với mặt phẳng (P).
HĐ 2
Video hướng dẫn giải
Cho đường thẳng a song song với mặt phẳng (P). Lấy hai điểm M, N bất kì thuộc a và gọi A, B tương ứng là các hình chiếu của chúng trên (P) (H.7.78).
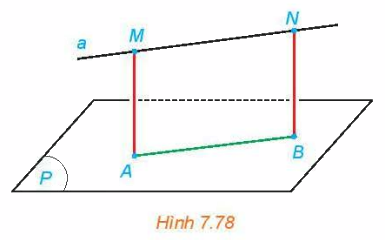
Giải thích vì sao ABNM là một hình chữ nhật và M, N có cùng khoảng cách đến (P).
Phương pháp giải:
- Nếu đường thẳng a song song với (P) thì mọi mặt phẳng (Q) chứa a cắt (P) thì sẽ cắt theo một giao tuyến song song với a.
- Hình bình hành có 1 góc vuông là hình chữ nhật.
Lời giải chi tiết:
Ta có \(MA \bot \left( P \right)\) (A là hình chiếu của M trên (P))
\(NB \bot \left( P \right)\) (B là hình chiếu của N trên (P))
\( \Rightarrow \) MA // NB \( \Rightarrow \) 4 điểm M, A, B, N đồng phẳng
\(\left. \begin{array}{l}\left( {AMNB} \right) \cap \left( P \right) = AB\\a//\left( P \right)\end{array} \right\} \Rightarrow a//AB\)
\( \Rightarrow \) Tứ giác AMNB là hình bình hành.
Mà \(MA \bot AB\left( {MA \bot \left( P \right)} \right)\)
\( \Rightarrow \) Tứ giác AMNB là hình chữ nhật nên MA = NB
Vậy M, N có cùng khoảng cách đến (P).
HĐ 3
Video hướng dẫn giải
a) Cho hai đường thẳng m và n song song với nhau. Khi một điểm M thay đổi trên m thì khoảng cách từ nó đến đường thẳng n có thay đổi hay không?
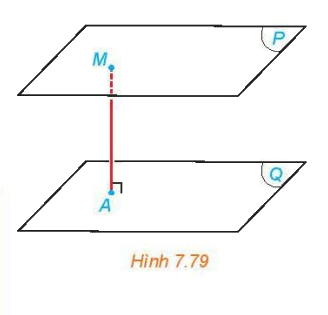
b) Cho hai mặt phẳng song song (P) và (Q) và một điểm M thay đổi trên (P) (H.7.79). Hỏi khoảng cách từ M đến (Q) thay đổi thế nào khi M thay đổi.

Phương pháp giải:
Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm bất kì trên a đến (P).
Lời giải chi tiết:
a) Khi một điểm M thay đổi trên đường thẳng m, khoảng cách từ M đến đường thẳng n không thay đổi vì m // n.
b) Vì (P) // (Q) nên các đường thẳng trên mặt (P) đều song song với (Q).
Dựa vào kết quả của hoạt động 2 ta có khi một điểm M thay đổi trên mặt phẳng (P), khoảng cách từ M đến mặt phẳng (Q) không thay đổi.
CH 1
Video hướng dẫn giải
Nếu đường thẳng a thuộc mặt phẳng (P) và mặt phẳng (Q) song song với (P) thì giữa d(a, (Q)) và d((P),(Q)) có mối quan hệ gì?
Phương pháp giải:
- Khoảng cách giữa hai mặt phẳng song song (P) và (Q) là khoảng cách từ một điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia.
- Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm bất kì trên a đến (P).
Lời giải chi tiết:
Gọi M là 1 điểm thuộc a mà a thuộc (P) nên M thuộc (P)
+) a // (Q) nên d(a, (Q)) = d(M, (Q))
+) (P) // (Q) nên d((P),(Q)) = d(M,(Q))
\( \Rightarrow \) d(a, (Q)) = d((P),(Q))
LT 2
Video hướng dẫn giải
Cho hình chóp S.ABC có SA \( \bot \) (ABC), SA = h. Gọi M, N, P tương ứng là trung điểm của SA, SB, SC.
a) Tính d((MNP),(ABC)) và d(NP,(ABC)).
b) Giả sử tam giác ABC vuông tại B và AB = a. Tính d(A,(SBC)).

Phương pháp giải:
- Khoảng cách giữa hai mặt phẳng song song (P) và (Q) là khoảng cách từ một điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia.
- Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm bất kì trên a đến (P).
Lời giải chi tiết:
a) +) Xét tam giác SBC có
N, P lần lượt là trung điểm SB, SC
\( \Rightarrow \) PN là đường trung bình tam giác SBC
\( \Rightarrow \) PN // BC \( \Rightarrow \) PN // (ABC)
+) Xét tam giác SAB có
N, M lần lượt là trung điểm SB, SA
\( \Rightarrow \) MN là đường trung bình tam giác SAB
\( \Rightarrow \) MN // AB
+) \(\left. \begin{array}{l}PN//BC,MN//AB\\PN \cap MN = \left\{ N \right\},BC \cap AB = \left\{ B \right\}\end{array} \right\} \Rightarrow \left( {MNP} \right)//\left( {ABC} \right)\)
\( \Rightarrow \) d((MNP), (ABC)) = d(M, (ABC)) = MA \( = \frac{{SA}}{2} = \frac{h}{2}\) do SA \( \bot \) (ABC)
+) PN // (ABC) \( \Rightarrow \) d(NP,(ABC)) = d(N,(ABC)) = d(M,(ABC))\( = \frac{h}{2}\) (do MN // (ABC))
b)
Ta có \(SA \bot BC,AB \bot BC \Rightarrow BC \bot \left( {SAB} \right);BC \subset \left( {SBC} \right) \Rightarrow \left( {SAB} \right) \bot \left( {SBC} \right)\)
\(\left( {SAB} \right) \cap \left( {SBC} \right) = SB\)
(SAB): kẻ \(AH \bot SB\)
\( \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow \) d(A,(SBC)) = AH
Xét tam giác SAB vuông tại A có
\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} = \frac{1}{{{h^2}}} + \frac{1}{{{a^2}}} = \frac{{{a^2} + {h^2}}}{{{h^2}{a^2}}} \Rightarrow AH = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
Vậy \(d\left( {A,\left( {SBC} \right)} \right) = \frac{{ah}}{{\sqrt {{a^2} + {h^2}} }}\)
VD
Video hướng dẫn giải
Ở một con dốc lên cầu, người ta đặt một khung khống chế chiều cao, hai cột của khung có phương thẳng đứng và có chiều dài bằng 2,28 m. Đường thẳng nối hai chân cột vuông góc với hai đường mép dốc. Thanh ngang được đặt trên đỉnh hai cột. Biết dốc nghiêng 150 so phương nằm ngang. Tính khoảng cách giữa thanh ngang của khung và mặt đường (theo đơn vị mét và làm tròn kết quả đến chữ số thập phân thứ hai). Hỏi cầu này có cho phép xe cao 2,21 m đi qua hay không?

Phương pháp giải:
Tính cạnh góc vuông bằng cạnh huyền nhân sin góc đối
Lời giải chi tiết:

Gọi B là một điểm nằm trên thanh ngang và H là hình chiếu vuông góc xuống mặt dốc.
Vì dốc nghiêng 150 so với phương nằm ngang nên nên góc giữa cột và mặt phẳng dốc bằng 750
Khoảng cách từ B đến mặt phẳng dốc là \(BH = 2,28.\sin {75^0} \approx 2,2\left( m \right).\)
Do đó không cho phép xe cao 2,21 m đi qua.
Giải mục 2 trang 55, 56, 57 SGK Toán 11 tập 2 - Kết nối tri thức: Tổng quan và Phương pháp giải
Mục 2 của SGK Toán 11 tập 2 Kết nối tri thức thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững lý thuyết, hiểu rõ các định nghĩa, định lý và công thức liên quan. Bài viết này sẽ cung cấp một hướng dẫn chi tiết về cách tiếp cận và giải quyết các bài tập trong mục 2 trang 55, 56, 57, đồng thời cung cấp các ví dụ minh họa cụ thể.
Nội dung chính của Mục 2 (trang 55, 56, 57)
Thông thường, mục 2 sẽ xoay quanh các chủ đề như:
- Đạo hàm của hàm số lượng giác
- Ứng dụng đạo hàm để khảo sát hàm số
- Bài toán tối ưu hóa
Hướng dẫn giải chi tiết các bài tập
Dưới đây là hướng dẫn giải chi tiết các bài tập trong mục 2 trang 55, 56, 57 SGK Toán 11 tập 2 Kết nối tri thức:
Bài 1: (Trang 55)
Đề bài: (Ví dụ: Tính đạo hàm của hàm số y = sin(2x) + cos(x))
Lời giải:
- Sử dụng công thức đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) * v'(x)
- Áp dụng công thức đạo hàm của sin(x) và cos(x)
- Kết quả: y' = 2cos(2x) - sin(x)
Bài 2: (Trang 56)
Đề bài: (Ví dụ: Tìm cực trị của hàm số y = x^3 - 3x + 2)
Lời giải:
- Tính đạo hàm bậc nhất y'
- Giải phương trình y' = 0 để tìm các điểm dừng
- Tính đạo hàm bậc hai y''
- Xác định cực đại, cực tiểu dựa vào dấu của y'' tại các điểm dừng
Bài 3: (Trang 57)
Đề bài: (Ví dụ: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x^2 - 4x + 5 trên đoạn [0; 3])
Lời giải:
- Tính đạo hàm y'
- Giải phương trình y' = 0 để tìm các điểm dừng
- Tính giá trị của hàm số tại các điểm dừng và tại các đầu mút của đoạn
- So sánh các giá trị để tìm giá trị lớn nhất và giá trị nhỏ nhất
Mẹo giải nhanh và hiệu quả
Để giải các bài tập về đạo hàm và ứng dụng đạo hàm một cách nhanh chóng và hiệu quả, các em nên:
- Nắm vững các công thức đạo hàm cơ bản
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau
- Sử dụng máy tính cầm tay để kiểm tra lại kết quả
Lưu ý quan trọng
Khi giải các bài tập về đạo hàm, các em cần chú ý đến:
- Miền xác định của hàm số
- Các điểm không xác định của hàm số
- Các điểm không đạo hàm được của hàm số
Tổng kết
Hy vọng rằng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải quyết các bài tập trong mục 2 trang 55, 56, 57 SGK Toán 11 tập 2 Kết nối tri thức. Chúc các em học tập tốt!
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ.