Giải bài 7 trang 67 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 7 trang 67 sách bài tập Toán 11 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết bài 7 trang 67 sách bài tập Toán 11 - Kết nối tri thức. Bài viết này sẽ giúp các em hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp kiến thức chính xác và dễ hiểu nhất.
Cho hình chóp (S.ABCD) có mặt phẳng (left( {SAB} right)) vuông góc với mặt đáy
Đề bài
Trong các mệnh đề sau, mệnh đề sai là
A. \(\mathop {\lim }\limits_{x \to {0^ - }} \frac{1}{x} = - \infty \)
B. \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{x} = + \infty \)
C. \(\mathop {\lim }\limits_{x \to {0^ - }} \frac{1}{{{x^2}}} = - \infty \)
D. \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{{\sqrt[3]{x}}} = + \infty \)
Phương pháp giải - Xem chi tiết
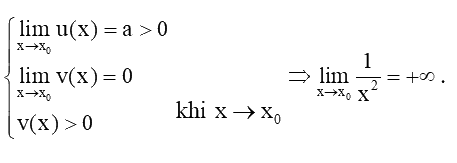
Lời giải chi tiết
Ta có:
\(\mathop {\lim }\limits_{x \to {0^ - }} {x^2} = 0\);
1 > 0;
\({x^2} > 0\) khi \(x \to {0^ - }\).
Suy ra \(\mathop {\lim }\limits_{x \to {0^ - }} \frac{1}{{{x^2}}} = + \infty \).
Giải bài 7 trang 67 SBT Toán 11 - Kết nối tri thức: Tổng quan
Bài 7 trang 67 sách bài tập Toán 11 - Kết nối tri thức tập trung vào việc vận dụng các kiến thức về phép biến hình affine để giải quyết các bài toán thực tế. Cụ thể, bài tập yêu cầu học sinh xác định các yếu tố của phép biến hình affine, tìm ảnh của một điểm hoặc một đường thẳng qua phép biến hình đó, và chứng minh các tính chất liên quan.
Nội dung chi tiết bài 7 trang 67 SBT Toán 11
Bài 7 bao gồm các câu hỏi và bài tập sau:
- Trong mặt phẳng Oxy, cho điểm A(1; 2). Tìm tọa độ điểm A' là ảnh của A qua phép biến hình affine f xác định bởi:
- f(x; y) = (x + 2y - 1; 3x - y + 2)
- Trong mặt phẳng Oxy, cho đường thẳng d: x + 2y - 3 = 0. Tìm phương trình đường thẳng d' là ảnh của d qua phép biến hình affine f xác định bởi:
- f(x; y) = (2x + y; x - y + 1)
- Cho tam giác ABC với A(0; 0), B(1; 0), C(0; 1). Tìm tọa độ các đỉnh của tam giác A'B'C' là ảnh của tam giác ABC qua phép biến hình affine f xác định bởi:
- f(x; y) = (x + y; 2x - y)
Phương pháp giải bài tập
Để giải các bài tập trong bài 7, học sinh cần nắm vững các kiến thức sau:
- Định nghĩa phép biến hình affine.
- Cách xác định các yếu tố của phép biến hình affine.
- Công thức tính tọa độ ảnh của một điểm qua phép biến hình affine.
- Cách tìm phương trình ảnh của một đường thẳng qua phép biến hình affine.
Lời giải chi tiết bài 7 trang 67 SBT Toán 11
Câu 1:
Để tìm tọa độ điểm A' là ảnh của A qua phép biến hình affine f, ta thay tọa độ của A vào công thức của f:
A'(x'; y') = f(1; 2) = (1 + 2*2 - 1; 3*1 - 2 + 2) = (4; 3)
Vậy, A'(4; 3).
Câu 2:
Để tìm phương trình đường thẳng d' là ảnh của d qua phép biến hình affine f, ta tìm ảnh của hai điểm thuộc d. Ví dụ, chọn điểm M(1; 1) thuộc d. Khi đó:
M'(x'; y') = f(1; 1) = (2*1 + 1; 1 - 1 + 1) = (3; 1)
Chọn điểm N(3; 0) thuộc d. Khi đó:
N'(x'; y') = f(3; 0) = (2*3 + 0; 3 - 0 + 1) = (6; 4)
Phương trình đường thẳng d' đi qua M'(3; 1) và N'(6; 4) là:
(y - 1) / (x - 3) = (4 - 1) / (6 - 3) = 1
y - 1 = x - 3
x - y - 2 = 0
Vậy, phương trình đường thẳng d' là x - y - 2 = 0.
Câu 3:
Tương tự như câu 2, ta tìm ảnh của các đỉnh A, B, C của tam giác ABC qua phép biến hình affine f:
A'(x'; y') = f(0; 0) = (0; 0)
B'(x'; y') = f(1; 0) = (1; 2)
C'(x'; y') = f(0; 1) = (1; -1)
Vậy, tọa độ các đỉnh của tam giác A'B'C' là A'(0; 0), B'(1; 2), C'(1; -1).
Lưu ý khi giải bài tập
Khi giải các bài tập về phép biến hình affine, cần chú ý:
- Kiểm tra kỹ công thức của phép biến hình affine.
- Chọn các điểm thích hợp để tìm ảnh của đường thẳng.
- Biểu diễn kết quả một cách chính xác và rõ ràng.
Hy vọng bài giải chi tiết này sẽ giúp các em hiểu rõ hơn về bài 7 trang 67 sách bài tập Toán 11 - Kết nối tri thức. Chúc các em học tập tốt!