Giải bài 4.52 trang 72 sách bài tập toán 11 - Kết nối tri thức với cuộc sống
Tổng quan nội dung
Giải bài 4.52 trang 72 SBT Toán 11 - Kết nối tri thức
Chào mừng các em học sinh đến với lời giải chi tiết bài 4.52 trang 72 sách bài tập Toán 11 Kết nối tri thức. Bài học này tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và phương pháp giải dễ hiểu nhất.
Chọn hình chóp S.ABCD có đáy ABCD là hình thang (AB//CD). Gọi d là giao tuyến của hai mặt phẳng (SAB) và (SCD).
Đề bài
Chọn hình chóp S.ABCD có đáy ABCD là hình thang (AB//CD). Gọi d là giao tuyến của hai mặt phẳng (SAB) và (SCD). Khi đó, d đi qua S và song song với
A. AC
B. CD
C. BD
D. BC
Phương pháp giải - Xem chi tiết
Nếu hai mặt phẳng chứa hai đường thẳng song song với nhau thì giao tuyến của chúng (nếu có) song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó.
Lời giải chi tiết
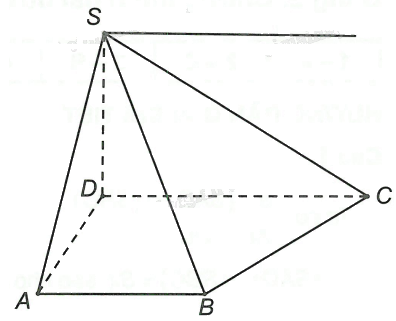
Đáp án B.
Vì AB//CD, CD nằm trong mặt phẳng (SCD) và S là giao điểm của hai mặt phẳng (SAB) và (SCD).
Do đó, giao tuyến d là đường thẳng d qua S và song song với CD.
Giải bài 4.52 trang 72 SBT Toán 11 - Kết nối tri thức: Hướng dẫn chi tiết
Bài 4.52 trang 72 sách bài tập Toán 11 Kết nối tri thức yêu cầu học sinh vận dụng kiến thức về đạo hàm của hàm số để giải quyết các bài toán liên quan đến tốc độ thay đổi của đại lượng. Dưới đây là lời giải chi tiết và hướng dẫn giải bài tập này:
Đề bài:
Một vật chuyển động theo quy luật s(t) = t3 - 3t2 + 5t + 2, trong đó s(t) là quãng đường đi được (tính bằng mét) sau thời gian t (tính bằng giây). Tính vận tốc của vật tại thời điểm t = 2 giây.
Lời giải:
Để tính vận tốc của vật tại thời điểm t = 2 giây, ta cần tìm đạo hàm của hàm s(t) theo t, tức là s'(t). Đạo hàm s'(t) biểu thị vận tốc của vật tại thời điểm t.
s'(t) = d/dt (t3 - 3t2 + 5t + 2) = 3t2 - 6t + 5
Thay t = 2 vào s'(t), ta được:
s'(2) = 3(2)2 - 6(2) + 5 = 12 - 12 + 5 = 5
Vậy, vận tốc của vật tại thời điểm t = 2 giây là 5 m/s.
Giải thích chi tiết:
- Bước 1: Xác định hàm quãng đường s(t) = t3 - 3t2 + 5t + 2.
- Bước 2: Tìm đạo hàm s'(t) của hàm s(t). Đạo hàm này biểu diễn vận tốc của vật tại thời điểm t.
- Bước 3: Thay t = 2 vào s'(t) để tính vận tốc tại thời điểm t = 2 giây.
Mở rộng kiến thức:
Bài toán này minh họa ứng dụng của đạo hàm trong việc tính tốc độ thay đổi của một đại lượng. Trong vật lý, đạo hàm của quãng đường theo thời gian chính là vận tốc, và đạo hàm của vận tốc theo thời gian là gia tốc.
Các bài tập tương tự:
Để củng cố kiến thức, các em có thể luyện tập thêm các bài tập tương tự về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Các bài tập này thường yêu cầu tính vận tốc, gia tốc, hoặc tìm điểm cực trị của hàm số.
Lưu ý quan trọng:
Khi giải các bài toán về đạo hàm, cần nắm vững các quy tắc tính đạo hàm cơ bản và hiểu rõ ý nghĩa vật lý của đạo hàm. Việc vẽ đồ thị hàm số cũng có thể giúp các em hình dung rõ hơn về sự thay đổi của hàm số và tìm ra lời giải chính xác.
Tusach.vn - Đồng hành cùng học sinh
Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho tất cả các bài tập trong sách giáo khoa và sách bài tập Toán 11 Kết nối tri thức. Hãy truy cập tusach.vn để được hỗ trợ tốt nhất trong quá trình học tập!
| Khái niệm | Giải thích |
|---|---|
| Đạo hàm | Tốc độ thay đổi tức thời của một hàm số tại một điểm. |
| Vận tốc | Tốc độ thay đổi của quãng đường theo thời gian. |
| Gia tốc | Tốc độ thay đổi của vận tốc theo thời gian. |